8759
TOPICS
LATEST
ABOUT
AUTHORING AREA
PARTICIPATE
Your browser does not support JavaScript or it may be disabled!
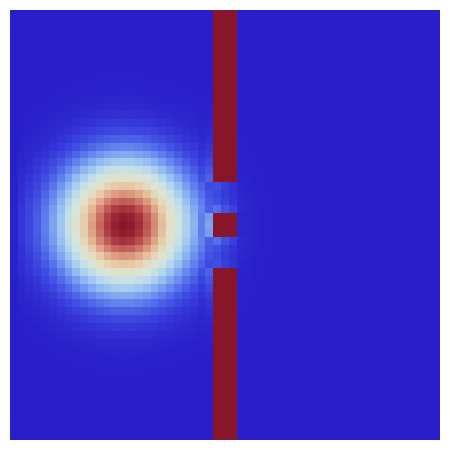
Probability Density for an Electron Passing through Two Narrow Slits
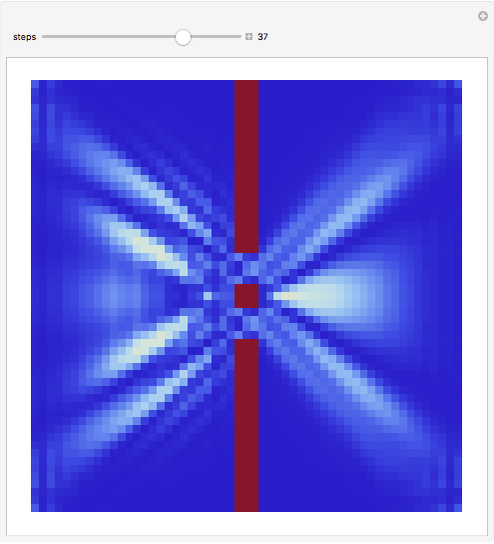
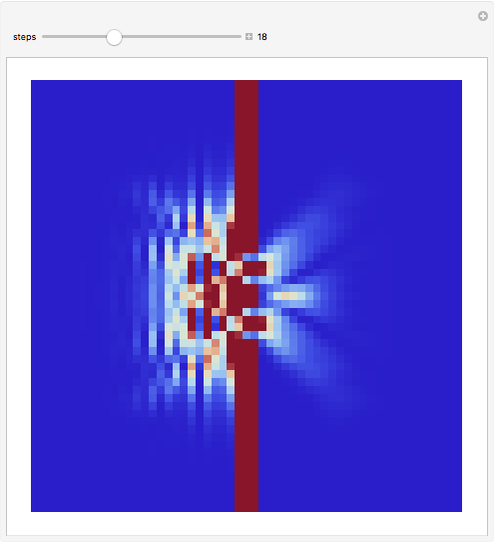
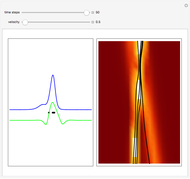
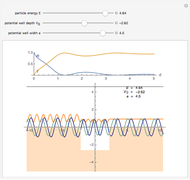
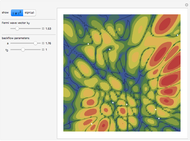
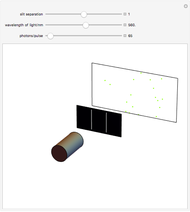
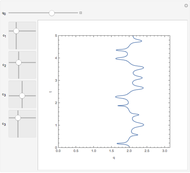
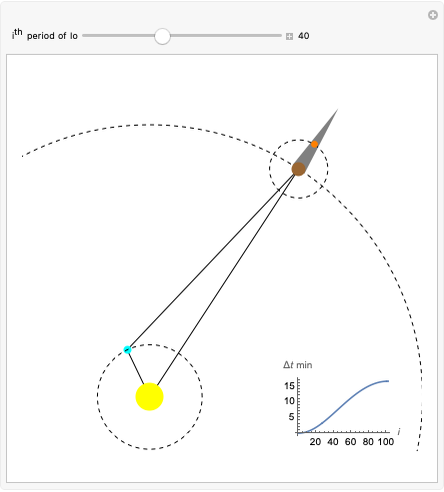
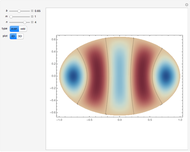
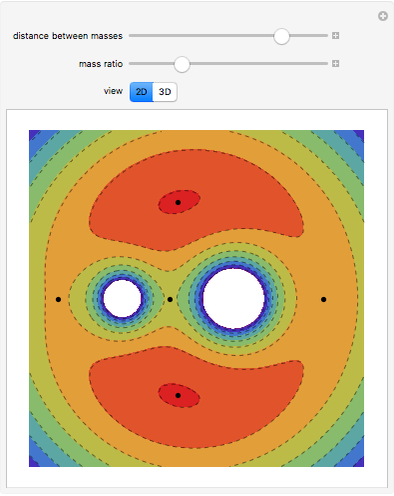
This Demonstration shows the quantum mechanical probability distribution of an electron passing through two narrow slits, which produces an interference pattern.
Contributed by:
Enrique Zeleny
Based on a program by:
Paul Nylander
THINGS TO TRY
Slider Zoom
Gamepad Controls
Automatic Animation
SNAPSHOTS
DETAILS
The finite-difference Crank–Nicolson method with time-splitting is used to solve the Schrödinger equation.
For more information, see the Wikipedia entry for "
Crank–Nicolson method
".
Reference
[1] B. Thaller,
Visual Quantum Mechanics
, New York: Springer-TELOS, 2000.
RELATED LINKS
Quantum Mechanics
(
ScienceWorld
)
Electron
(
ScienceWorld
)
Wavefunction
(
ScienceWorld
)
Probability Density
(
ScienceWorld
)
Schrödinger Equation
(
ScienceWorld
)
Finite Difference
(
Wolfram
MathWorld
)
PERMANENT CITATION
Enrique Zeleny
"
Probability Density for an Electron Passing through Two Narrow Slits
"
http://demonstrations.wolfram.com/ProbabilityDensityForAnElectronPassingThroughTwoNarrowSlits/
Wolfram Demonstrations Project
Published: July 16, 2012
Share:
Embed Interactive Demonstration
New!
Just copy and paste this snippet of JavaScript code into your website or blog to put the live Demonstration on your site.
More details »
Download Demonstration as CDF »
Download Author Code »
(preview »)
Files require
Wolfram
CDF Player
or
Mathematica
.
Related Demonstrations
More by Author
Causal Interpretation for an Electron Passing through Two Narrow Slits
Klaus von Bloh
Two-Soliton Collision for the Gross-Pitaevskii Equation in the Causal Interpretation
Klaus von Bloh
Scattering by a Square-Well Potential
M. Hanson
Dressed Multi-Particle Electron Wave Functions
Michael Trott with permission of Springer
Wave-Particle Duality in the Double-Slit Experiment
S. M. Blinder
Harmonic Oscillator Eigenfunctions
Michael Trott
Bohm Trajectories
Michael Trott
Harmonic Oscillator in a Half-space with a Moving Wall
Michael Trott
Wave Functions of Identical Particles
Michael Trott
Eigenfunctions of the Helmholtz Equation in a Right Triangle
Michael Trott
Related Topics
Quantum Physics
Waves
Browse all topics
Note: To run this Demonstration you need Mathematica 7+ or the free Mathematica Player 7EX
Download or upgrade to
Mathematica Player 7EX
I already have
Mathematica Player
or
Mathematica 7+
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
