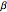Property Coinsurance

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Property insurance frequently contains a "coinsurance clause" stating that, if the insured values its property at some fraction  of its actual value
of its actual value  , and
, and  is less than a coinsurance percentage
is less than a coinsurance percentage  (often 80%), the insurer may reduce its payment to
(often 80%), the insurer may reduce its payment to 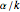 of the loss. By way of example, if a house were insured for $140,000, which was a fraction 0.7 of its actual value of $200,000, and the coinsurance percentage were 0.8, the insurer would have to pay only $70,000 following an insured $80,000 loss to the insured. This provision is intended to deter deliberate underinsurance of property, which can work to the insurer's disadvantage when premiums are a linear function of the value the insured places on the property.
of the loss. By way of example, if a house were insured for $140,000, which was a fraction 0.7 of its actual value of $200,000, and the coinsurance percentage were 0.8, the insurer would have to pay only $70,000 following an insured $80,000 loss to the insured. This provision is intended to deter deliberate underinsurance of property, which can work to the insurer's disadvantage when premiums are a linear function of the value the insured places on the property.
Contributed by: Seth J. Chandler (April 2007)
Open content licensed under CC BY-NC-SA
Snapshots
Details
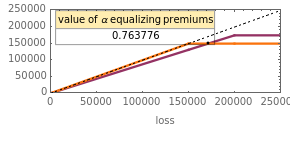
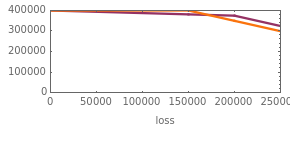
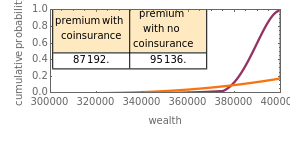
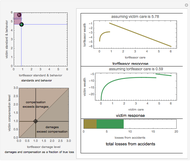
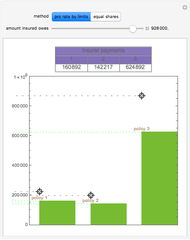
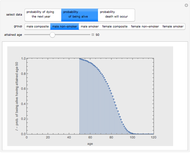
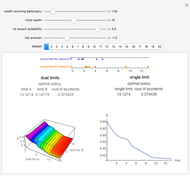
The policies will have the same premium if the areas under the curves in the bottom-most wealth distribution graphic are equal to each other. Assuming that the insured is risk averse and the premiums for the policies are the same, the insured will prefer the less "disperse" wealth distribution curve, which ends up always being the curve generated by an insurance policy with a coinsurance requirement. Professor Venezia's original article setting forth this model may be found in The Journal of Risk and Insurance, 55(2) 1988 pp. 307-314. The graphics go black if the constraint 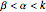 is violated.
is violated.
The top panel contains an inset identifying the fraction of property value insured when coinsurance is present that will cost the insured the same premium as the policy with a lower fraction of property value insured but without coinsurance. The policy with coinsurance will yield a risk averse insured greater utility than the equally priced policy without coinsurance.
Snapshot 1: a different loss distribution function and a low coinsurance requirement
Snapshot 2: the same loss distribution function as in Snapshot 1 but with a high coinsurance requirement and low α
Snapshot 3: a loss distribution function with a high first parameter and low second parameter
Permanent Citation