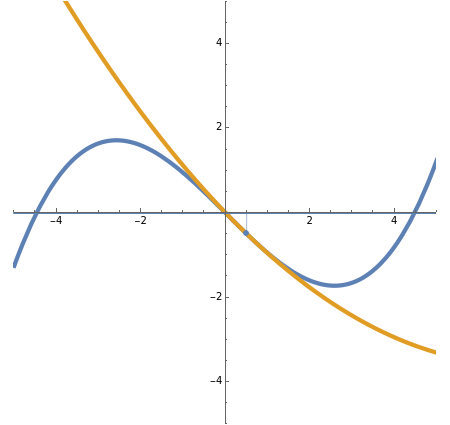
Quadratics Tangent to a Cubic

This Demonstration shows a cubic polynomial, which you can modify using the locators, and a quadratic polynomial that is tangent to the cubic at the point determined by the slider. That the family of quadratics parametrized by the point of tangency do not intersect and fill the plane is the content of an amazing theorem referenced in the details below.