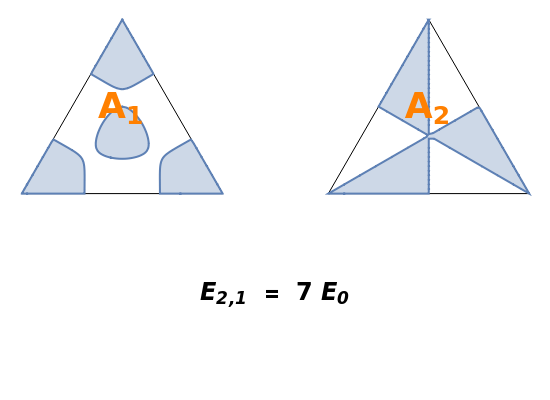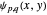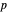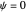Quantum-Mechanical Particle in an Equilateral Triangle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
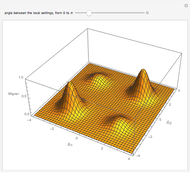
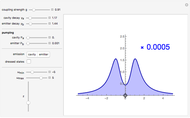
The particle in an equilateral triangle is the simplest quantum-mechanical problem that has a nonseparable but exact analytic solution. The Schrödinger equation can be written 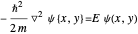 with
with 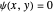 on and outside an equilateral triangle of side
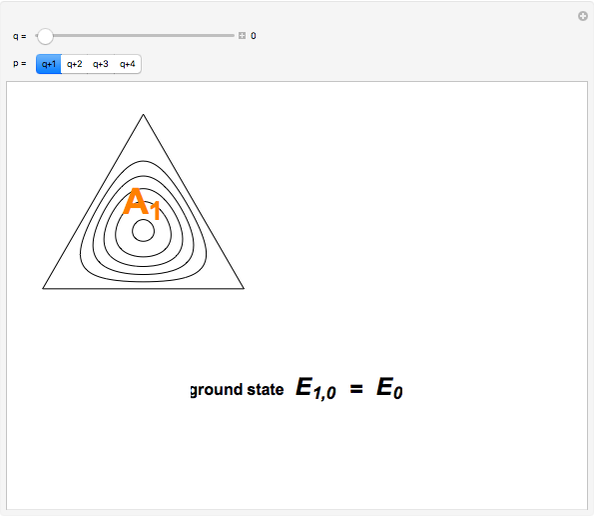
on and outside an equilateral triangle of side 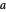 . The ground-state solution
. The ground-state solution 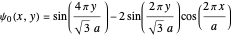 corresponds to an energy eigenvalue
corresponds to an energy eigenvalue 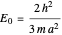 . The general solutions have the form
. The general solutions have the form 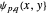 with
with 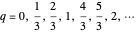 and
and 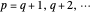 , with energies
, with energies 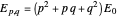 . The Hamiltonian transforms under the symmetry group
. The Hamiltonian transforms under the symmetry group 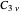 so eigenfunctions belong to one of the irreducible representations
so eigenfunctions belong to one of the irreducible representations 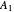 ,
, 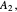 or
or 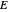 . The states labeled by quantum numbers
. The states labeled by quantum numbers 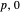 , including the ground state
, including the ground state 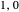 , are nondegenerate with symmetry
, are nondegenerate with symmetry 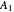 . All other integer combinations
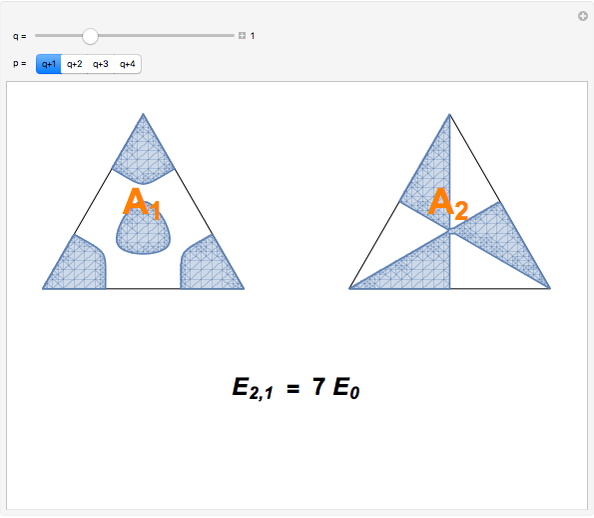
. All other integer combinations 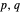 give degenerate pairs of
give degenerate pairs of 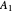 and
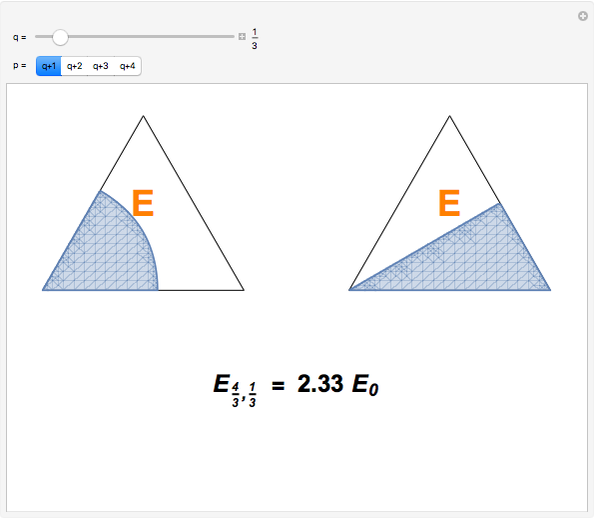
and 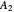 states. Noninteger quantum numbers belong to twofold degenerate
states. Noninteger quantum numbers belong to twofold degenerate 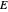 levels.
levels.
Contributed by: Wai-Kee Li (Chinese University of Hong Kong) and S. M. Blinder (April 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
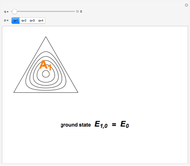
Snapshot 1: contour plot of ground state
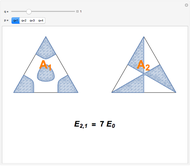
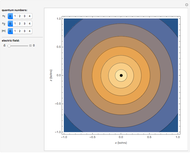
Snapshot 2: degenerate pair of 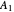 ,
, 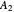 states
states
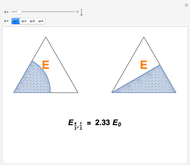
Snapshot 3: lowest-energy 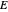 states
states
Reference: W.-K. Li and S. M. Blinder, "Solution of the Schrödinger Equation for a Particle in an Equilateral Triangle," Journal of Mathematical Physics, 26(11), 1985 pp. 2784–2786.
Permanent Citation