Raising the Degree for Bézier Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
A Bézier curve in the plane is given by parametric equations of the form 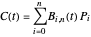 , where
, where 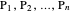 are points in the plane called control points and
are points in the plane called control points and 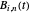
 is the
is the 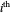 Bernstein polynomial of degree
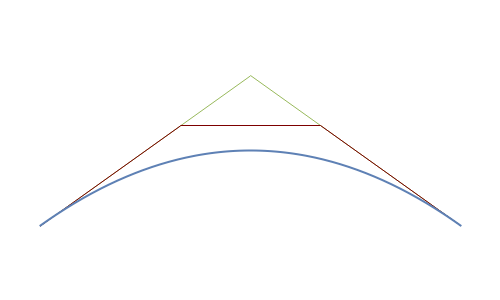
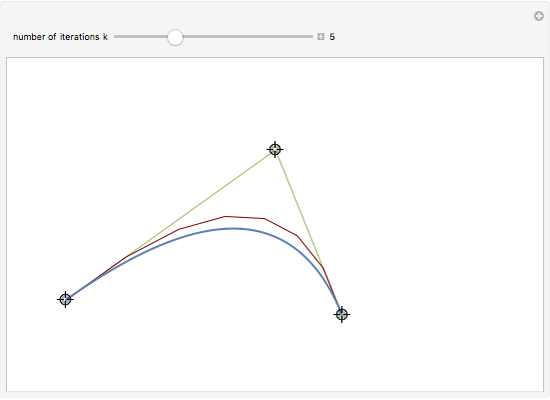
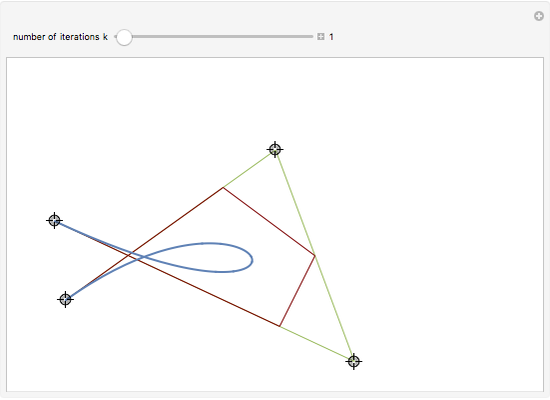
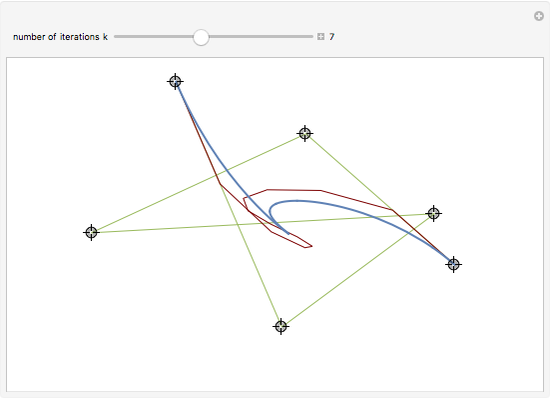
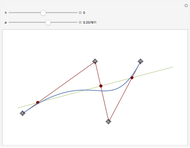
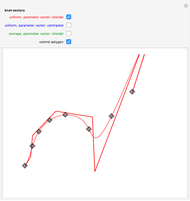
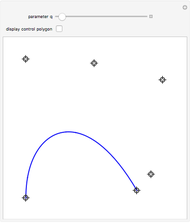
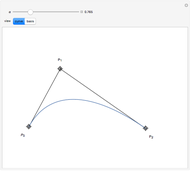
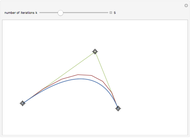
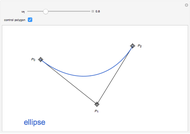
Bernstein polynomial of degree 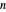 . This parametrization can be changed (without changing the curve) via a recursive procedure outlined in the Details section that generates a new set of control points larger by 1 at each iteration. The figure shows the Bézier curve, the original control polygon (obtained by connecting the control points with line segments), and the control polygon determined by the control points after some iterations of the recursive procedure. This artificial process is useful in CAGD to increase the flexibility for the designer. It may also be used in numerous contexts where several Bézier curves need to be represented with the same degree, for example to join two curves by a Bézier surface, or to compare two curves, etc.
. This parametrization can be changed (without changing the curve) via a recursive procedure outlined in the Details section that generates a new set of control points larger by 1 at each iteration. The figure shows the Bézier curve, the original control polygon (obtained by connecting the control points with line segments), and the control polygon determined by the control points after some iterations of the recursive procedure. This artificial process is useful in CAGD to increase the flexibility for the designer. It may also be used in numerous contexts where several Bézier curves need to be represented with the same degree, for example to join two curves by a Bézier surface, or to compare two curves, etc.
Contributed by: Isabelle Cattiaux-Huillard and Gudrun Albrecht (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A Bézier curve is defined by
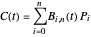 ,
,
where the 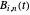 are the Bernstein polynomials. Applying the following recursive formula for the control points raises the degree of the Bernstein basis:
are the Bernstein polynomials. Applying the following recursive formula for the control points raises the degree of the Bernstein basis:
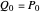 ,
,
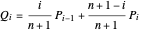 , for
, for 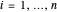 ,
,
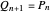 .
.
The curve 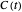 can then be parametrized by
can then be parametrized by
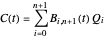 .
.
Indeed:
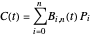
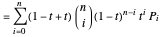
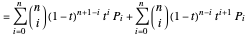
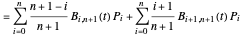
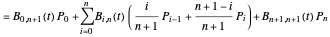
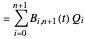 .
.
Although the curve has a new control polygon, its parametrization remains the same. For further details, see:
G. Farin, Curves and Surfaces for Computer Aided Geometric Design, Boston: Academic Press, 1992.
Permanent Citation