Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Random Domino Tilings

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

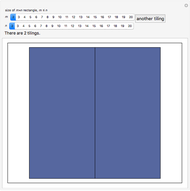
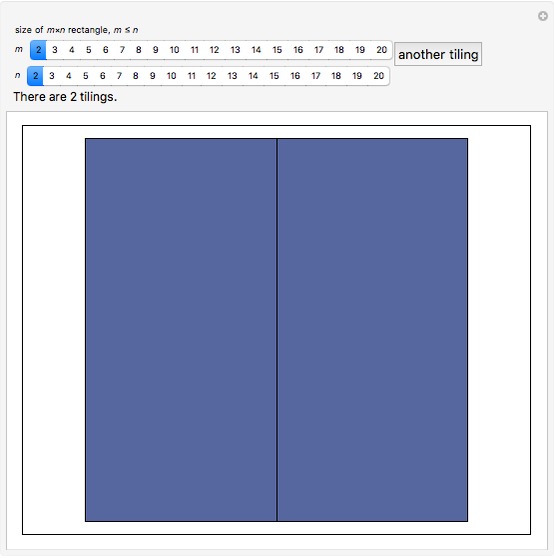
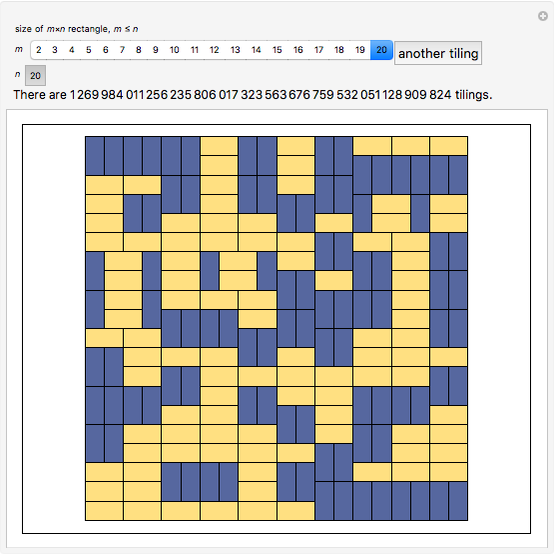
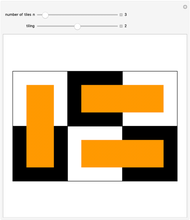
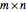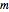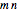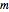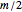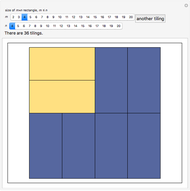
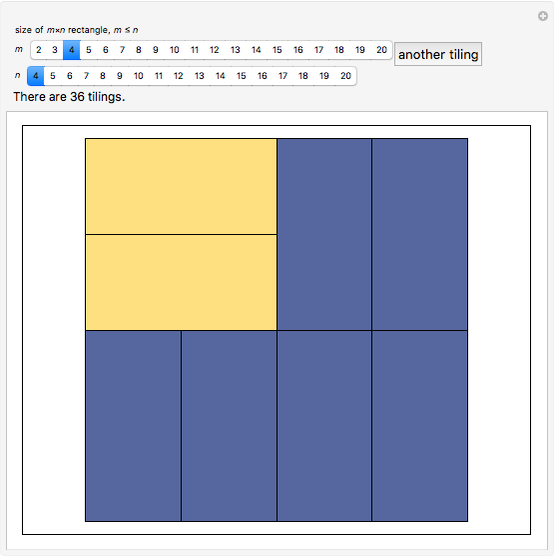
Consider an rectangle and rectangular tiles of size 1×2 (dominoes). A domino tiling of the rectangle is a placement of dominoes that covers the rectangle completely without overlaps. A tiling exists if and only if and are not both odd, implying is even. One tiling can readily be found: suppose is even, place dominoes vertically in the first column and repeat for the next columns. This Demonstration generates random tilings of rectangles of chosen sizes and computes the total number of tilings possible.

Contributed by: Jaime Rangel-Mondragon (July 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

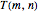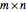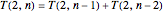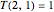If is the number of tilings of an rectangle, it is easy to see that . As and 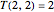, 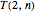is a Fibonacci number. The original motivation for tackling the tiling problem by dominoes (or dimers) was to provide a simple model to describe the thermodynamic behavior of fluids. The amazing formula for 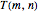was first obtained by Kasteleyn in 1961: 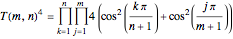, which is the formula used in this Demonstration.

References

[1] P. Kasteleyn, "The Statistics of Dimers on a Lattice I. The Number of Dimer Arrangements in a Quadratic Lattice," Physica, 27, 1961 pp. 1209–1225.

[2] R. Kenyon and A. Okounkov, "What Is...a Dimer?" Notices of the American Mathematical Society, 52(3), 2005 pp. 342–343.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send