Mathematica MathWorld Wolfram Science More »

Rational Number Explorer

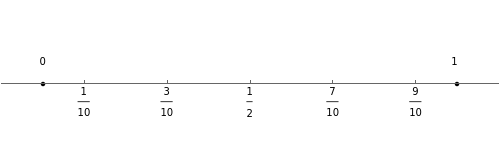
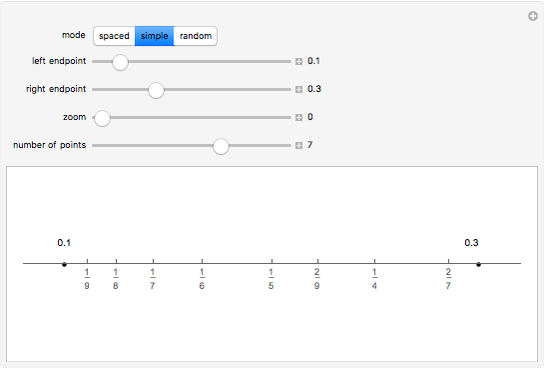
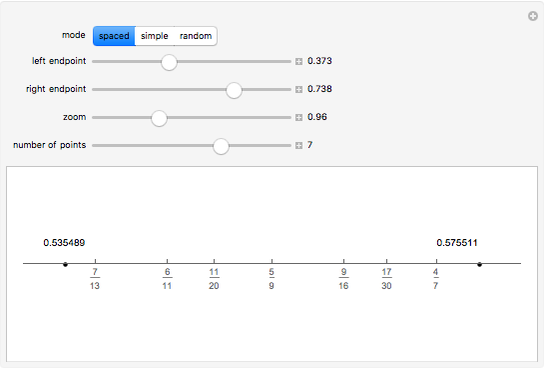
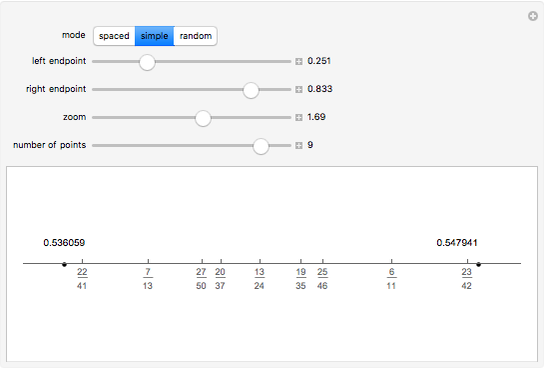
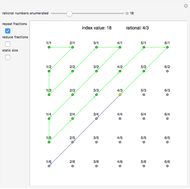
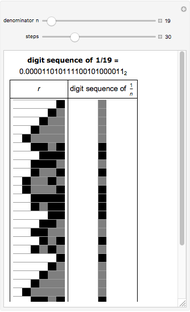
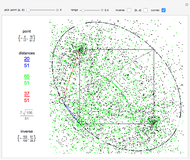
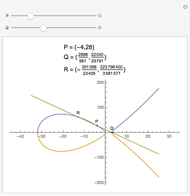
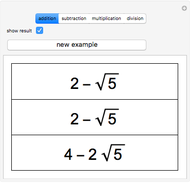
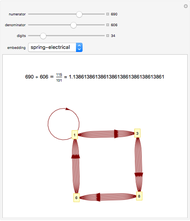
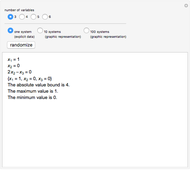
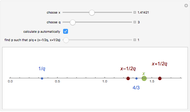
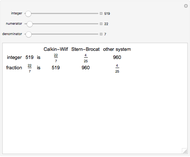
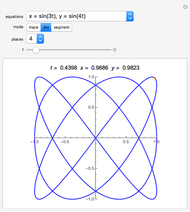
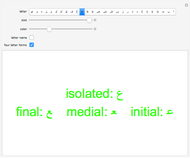
Rational numbers ("fractions") are often more difficult to understand than decimal numbers. Use this explorer to get a feeling for them.

Tricky Questions to think about!

How many rational numbers are there between 0 and 1?

What is the smallest rational number which is larger than 0?

How close together can rational numbers get?

Can you always find a rational number between any two decimal numbers?

Can you use this explorer to find a decimal approximation for

? (

is approximately 3.14159.)

(9 lines omitted)

Contributed by: Richard Mercer

Report an issue »

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

RSS

Atom