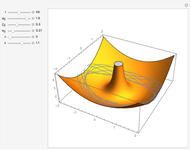
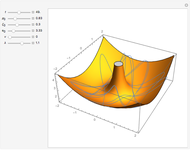
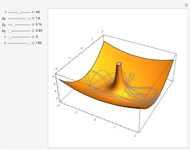
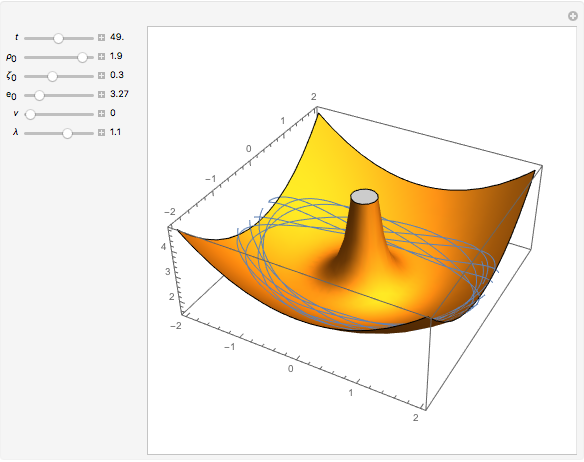
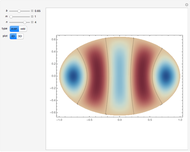
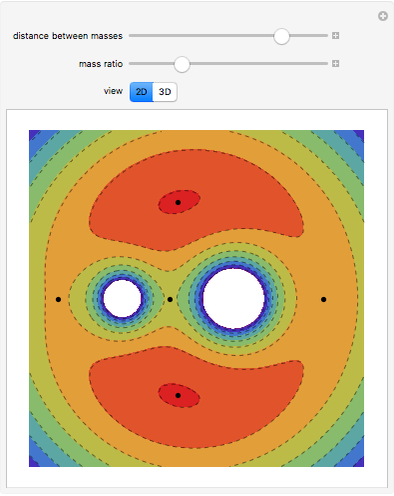
Relative Motion for Two Ions in a Penning Trap

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
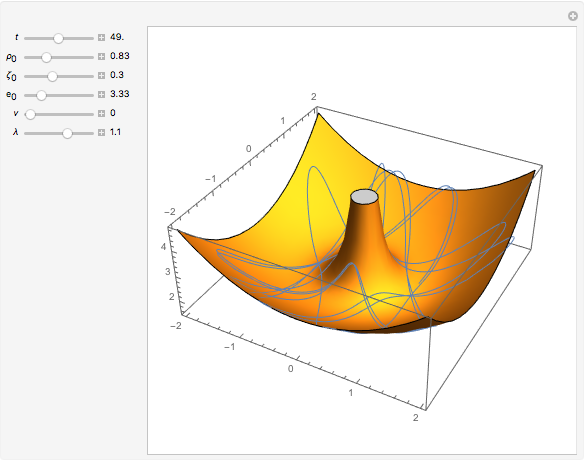
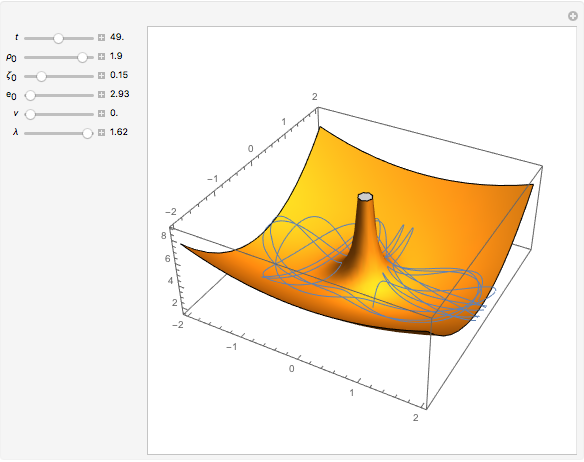
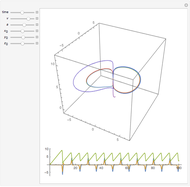
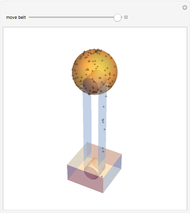
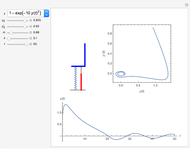
A Penning trap uses a combination of electric and magnetic fields to confine ions in a cavity bounded by paraboloids, creating quadrupole fields. The plot shows the path for two ions for initial conditions 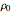 and
and 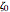 with energy
with energy 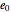 .
.
Contributed by: Enrique Zeleny (October 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The equations for the Coulomb forces between the two ions and the Lorentz force from a constant magnetic field in the  direction can be decoupled by introducing relative coordinates
direction can be decoupled by introducing relative coordinates 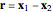 ,
,
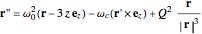 ,
,
where 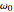 and
and 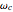 are characteristic frequencies and
are characteristic frequencies and 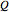 a scaled charge. Using cylindrical coordinates, the variables can be separated. Introducing a conserved quantity for the
a scaled charge. Using cylindrical coordinates, the variables can be separated. Introducing a conserved quantity for the  -angular dependence, and simplifying yields the equations of motion
-angular dependence, and simplifying yields the equations of motion
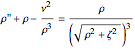 ,
,
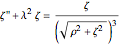 .
.
This gives an effective potential
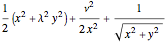
with parameters  and
and 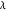 , the equations can be transformed to a system of four linear differential equations with the variables
, the equations can be transformed to a system of four linear differential equations with the variables  and
and  .
.
Reference
[1] G. Baumann, Mathematica for Theoretical Physics: Electrodynamics, Quantum Mechanics, General Relativity, and Fractals, 2nd ed., New York: Springer, 2005.
Permanent Citation