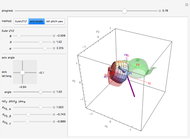
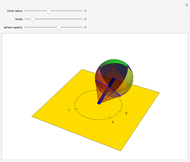
Roll Any Point on the Sphere to Any Desired Latitude-Longitude Coordinates with One Straight-Line Roll

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
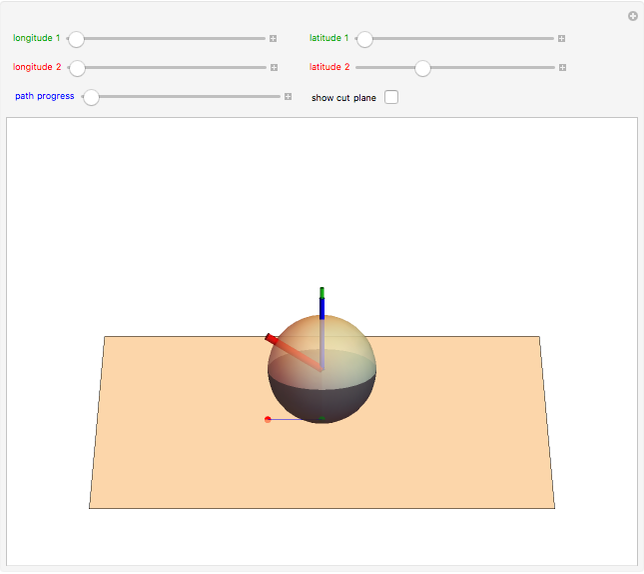
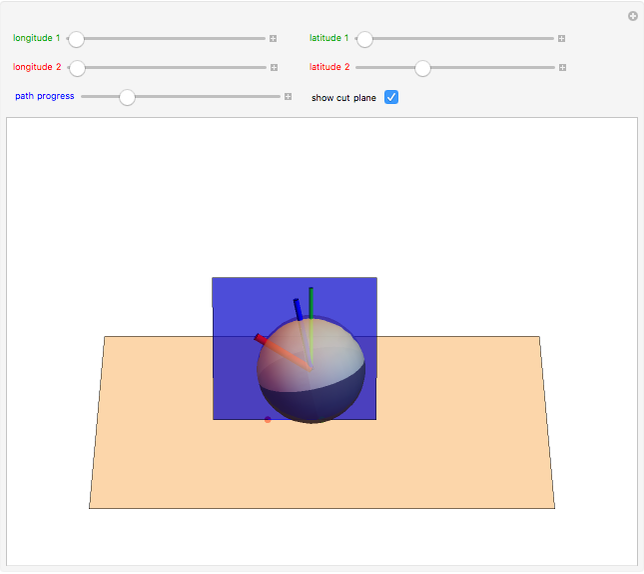
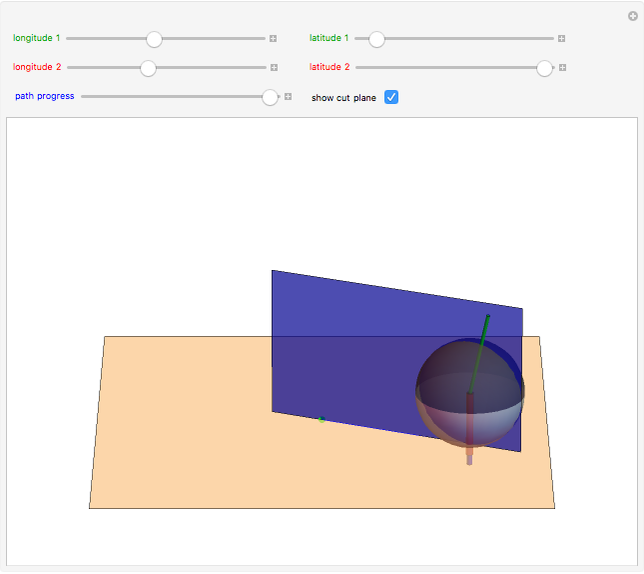
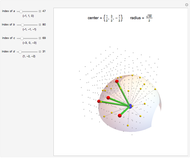
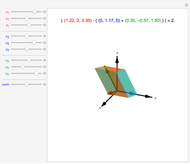
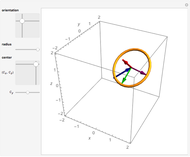
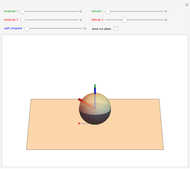
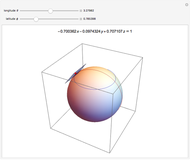
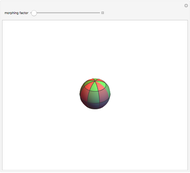
Pick a point on a sphere (in green). This point has certain latitude-longitude coordinates. In one straight-line roll, we can move this point to any desired latitude-longitude coordinates (in red). This Demonstration shows the shortest such roll.
Contributed by: Aaron Becker (October 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
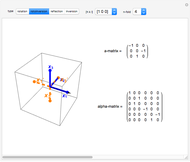
A roll in the horizontal plane of length 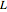 about an axis at angle
about an axis at angle  with the
with the  axis produces the following change in orientation:
axis produces the following change in orientation:
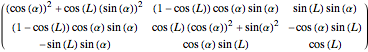 .
.
We want to choose the pair 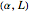 that moves a point from the starting latitude-longitude pair to the desired latitude-longitude pair.
that moves a point from the starting latitude-longitude pair to the desired latitude-longitude pair.
First, we compute the 3D location of the point from the latitude-longitude pair 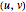 :
:
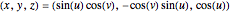 .
.
Let 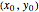 and
and 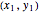 be the start and end coordinates.
be the start and end coordinates.
The angle to roll along is given by 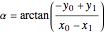 , which is undefined if the
, which is undefined if the 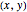 coordinates overlap. If they overlap and
coordinates overlap. If they overlap and 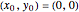 any angle works. Otherwise, set
any angle works. Otherwise, set 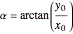 .
.
The length of the roll 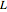 is determined by the angle between the start and ending latitude-longitude pair with respect to the intersection of the line in the
is determined by the angle between the start and ending latitude-longitude pair with respect to the intersection of the line in the  -
-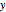 plane between the start and end points and a perpendicular line to the origin. If
plane between the start and end points and a perpendicular line to the origin. If 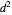 is the squared
is the squared  -
-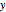 distance between the start and end points, this intersection point is given by
distance between the start and end points, this intersection point is given by
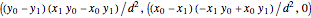 .
.
If 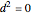 , the intersection point is the origin.
, the intersection point is the origin.
If 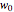 and
and 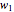 are the vectors to the starting and ending north poles from this intersection point, then we can use a property of the dot product to calculate the angle
are the vectors to the starting and ending north poles from this intersection point, then we can use a property of the dot product to calculate the angle 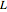 , which satisfies
, which satisfies 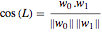 .
.
Permanent Citation