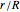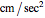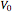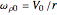Rolling Ball inside a Cylinder

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
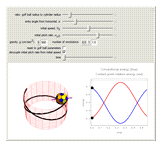
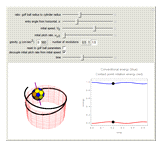
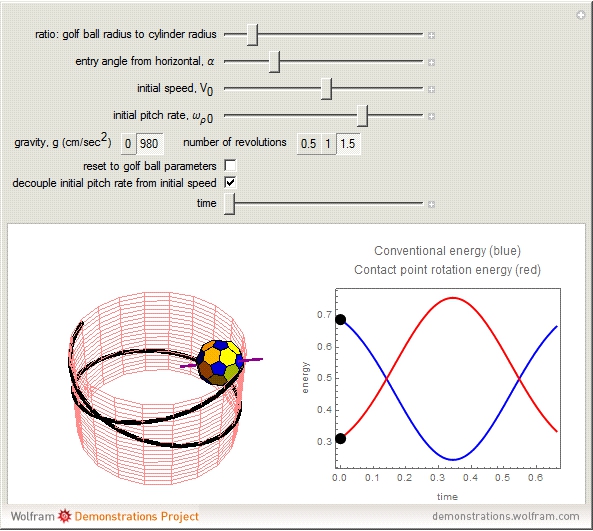
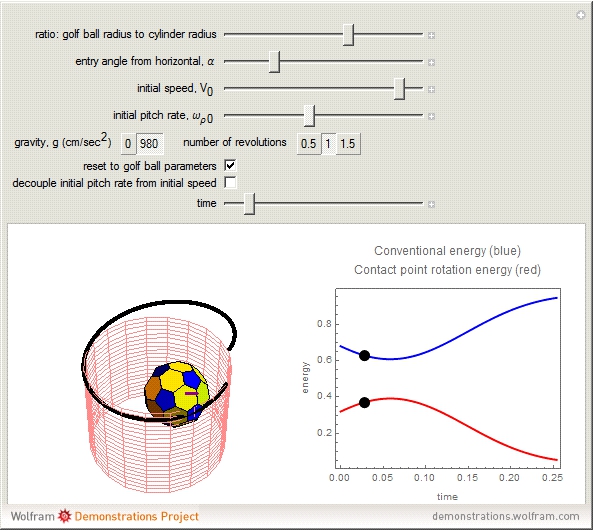
A ball rolling along the inside of a cylinder without slipping performs a surprising return to the starting height. This is related to the phenomenon of a golf ball rising out of the cup after it starts to fall in. This Demonstration uses the equations of motion to show the rolling ball together with the axis of rotation and an energy plot. A key point is the proper coordinate system for studying the axis of rotation. The rotation axis is given by 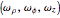 , where
, where  refers to the vertical axis through the center of the ball,
refers to the vertical axis through the center of the ball,  refers to the horizontal axis through the point of contact and normal to the cylinder, and
refers to the horizontal axis through the point of contact and normal to the cylinder, and  refers to the horizontal axis perpendicular to that of
refers to the horizontal axis perpendicular to that of  . The third component of the angular velocity,
. The third component of the angular velocity, 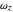 , turns out to remain constant. The graph on the right shows the breakdown of two types of energy. Total energy is constant, but the energy can be divided into a conventional part (kinetic energy plus angular energy due to rotation of
, turns out to remain constant. The graph on the right shows the breakdown of two types of energy. Total energy is constant, but the energy can be divided into a conventional part (kinetic energy plus angular energy due to rotation of 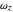 and
and 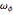 plus potential energy) and a surprising part, the spinning around the
plus potential energy) and a surprising part, the spinning around the  axis,
axis, 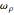 . The
. The 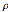 -spinning is due to a coriolis torque and it is this that causes the sign of
-spinning is due to a coriolis torque and it is this that causes the sign of 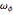 to reverse; because
to reverse; because 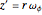 , the reversal of
, the reversal of  -spin causes the reversal of the
-spin causes the reversal of the  -motion.
-motion.
Contributed by: Dan Curtis (Central Washington University), Alexi Radovinsky, and Stan Wagon (Macalester College) (September 2009)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The physics of a ball rolling inside a cylinder is worked out in the paper by Gualtieri et al; they analyze the various forces involved, notably a Coriolis torque that acts around the  -axis. A physical demonstration of the process is described in the paper by Matsuura. We enhanced the work of Gualtieri et al by allowing an initial spinning
-axis. A physical demonstration of the process is described in the paper by Matsuura. We enhanced the work of Gualtieri et al by allowing an initial spinning 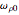 around the
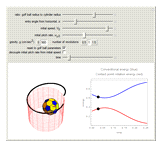
around the  -axis. This matches the behavior of a golf ball, which would be spinning at a rate proportional to its speed as it falls into the cup (see second snapshot). Solving the differential equations yields a formula of the form
-axis. This matches the behavior of a golf ball, which would be spinning at a rate proportional to its speed as it falls into the cup (see second snapshot). Solving the differential equations yields a formula of the form 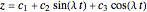 . But in order to learn where points are at time
. But in order to learn where points are at time  requires the numerical solution of a differential equation so that the angular velocity at each instant is as it should be. The angular velocity is computed from
requires the numerical solution of a differential equation so that the angular velocity at each instant is as it should be. The angular velocity is computed from 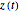 by the following equation, where
by the following equation, where  is the radius of the ball,
is the radius of the ball, 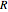 is the radius of the cylinder, and
is the radius of the cylinder, and 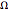 is a constant that represents the (negative of) the angular speed of the ball around the central axis of the cylinder:
is a constant that represents the (negative of) the angular speed of the ball around the central axis of the cylinder: 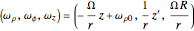 . Note that
. Note that 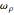 is a linear function of
is a linear function of  . The program for the soccer ball was taken from a Demonstration by Greg Wilhelm.
. The program for the soccer ball was taken from a Demonstration by Greg Wilhelm.
References:
M. Gualtieri, T. Tokieda, L. Advis-Gaete, B. Carry, E. Reffet, and C. Guthman, "Golfer's Dilemma," American Journal of Physics, 74(6), 2006 pp. 497–501.
A. Matsuura, "Strange Physical Motion of Balls in a Cylinder," Proc. of Bridges Conference, Banff, 2005.
Permanent Citation