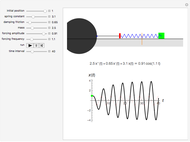
Runge-Kutta versus Velocity-Verlet Solutions for the Classical Harmonic Oscillator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
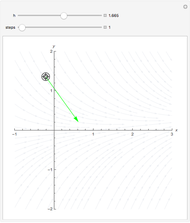
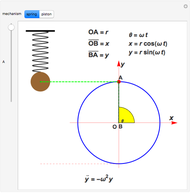
The harmonic oscillator is an idealized system widely used in many physical applications. It consists of a mass that oscillates without friction around an equilibrium position under a conservative attractive force. The energy is therefore constant. There is another conserved quantity, often not mentioned—the phase-space two-form 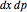 (where
(where  is a coordinate and
is a coordinate and 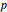 the conjugate momentum). The conservation of this quantity in a Hamiltonian system is a necessary and sufficient condition for conservation of the total number of particles, relevant if the system contains a fixed number of particles.
the conjugate momentum). The conservation of this quantity in a Hamiltonian system is a necessary and sufficient condition for conservation of the total number of particles, relevant if the system contains a fixed number of particles.
Contributed by: Luigi Tiburzi (April 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
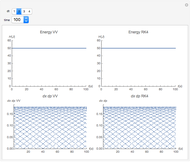
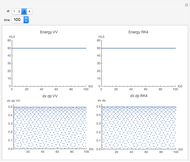
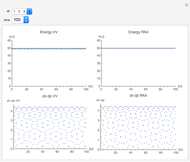
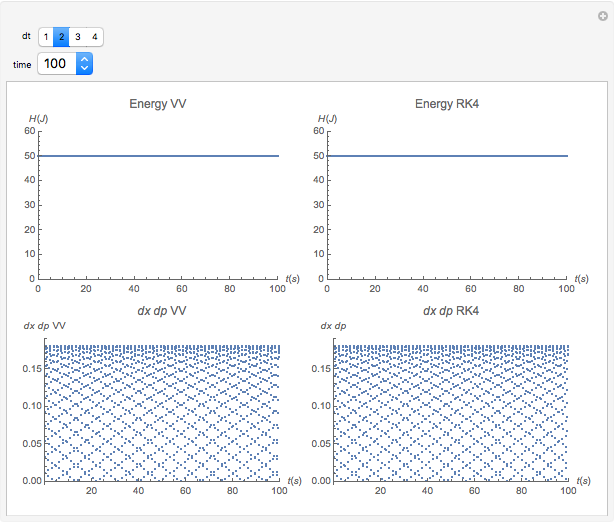
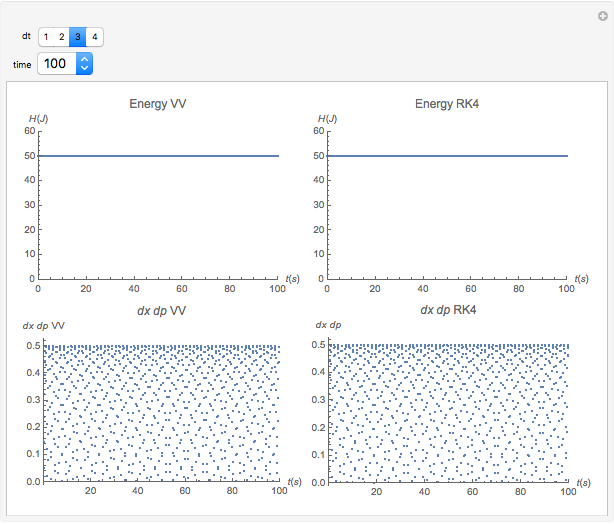
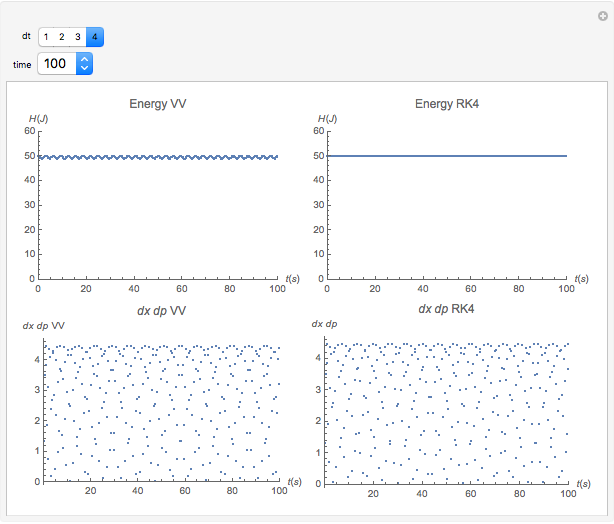
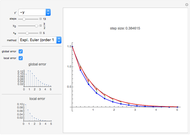
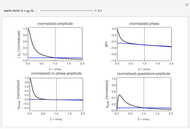
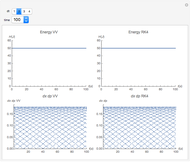
The Demonstration aims to simulate a classical molecular model for bond vibrations [1] in which the force fields [2] are approximated as harmonic oscillators [3]. Usually simulations are carried out in isolated conservative systems so it is important to have both energy and the total number of particles [4] conserved by the approximate solution. This is achieved by conservtion of the product 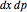 . In the above example you can see the best that can be achieved for the former product is a strongly oscillating value with a constant mean and not a single point constant value. This result is reached by the VV algorithm but not by the RK algorithm. Algorithms able to conserve
. In the above example you can see the best that can be achieved for the former product is a strongly oscillating value with a constant mean and not a single point constant value. This result is reached by the VV algorithm but not by the RK algorithm. Algorithms able to conserve 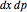 are referred to as symplectic integrators [5]. Typical molecular calculations are carried out with
are referred to as symplectic integrators [5]. Typical molecular calculations are carried out with 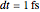 .
.
A typical real vibration has 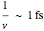 so the
so the 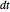 used in molecular dynamics to approximate the equations is roughly consistent with the width of a single vibration (or at least, the shortest vibration in the system).
used in molecular dynamics to approximate the equations is roughly consistent with the width of a single vibration (or at least, the shortest vibration in the system).
The harmonic oscillator in the simulation has 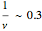 so the following values of
so the following values of 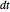 (in seconds) have been chosen: 0.01; 0.06; 0.1; 0.3.
(in seconds) have been chosen: 0.01; 0.06; 0.1; 0.3.
Increasing 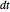 increases the difference in behavior of the two algorithms up to the
increases the difference in behavior of the two algorithms up to the 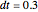 (at this value, molecular world and real world proportions are the same). It is clear that RK, not being a symplectic integrator, cannot be used as an algorithm to integrate the equation of motion in a molecular dynamics simulation.
(at this value, molecular world and real world proportions are the same). It is clear that RK, not being a symplectic integrator, cannot be used as an algorithm to integrate the equation of motion in a molecular dynamics simulation.
References
[1] Wikipedia. "Molecular Vibration." (Mar 27, 2012) en.wikipedia.org/wiki/Molecular_vibration.
[2] Wikipedia. "Force Field." (Apr 10, 2012) en.wikipedia.org/wiki/Force_field_(chemistry).
[3] Wikipedia. "Harmonic Oscillator." (Apr 5, 2012) en.wikipedia.org/wiki/Harmonic_oscillator.
[4] Wikipedia. "Liouville's Theorem." (Mar 18, 2012) en.wikipedia.org/wiki/Liouville's_theorem _(Hamiltonian).
[5] Wikipedia. "Symplectic Integrator." (Oct 27, 2011) en.wikipedia.org/wiki/Symplectic_integrator.
Permanent Citation