Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

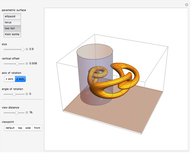
Sliding on a Parabolic Track

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

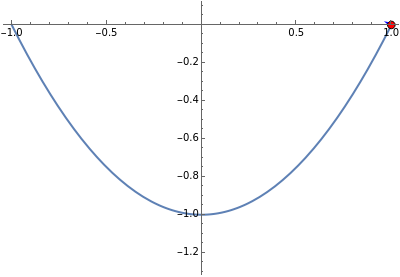
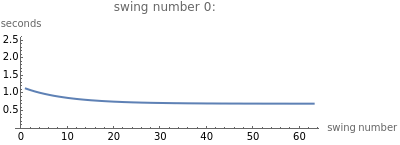
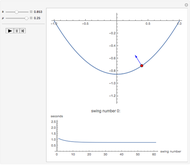
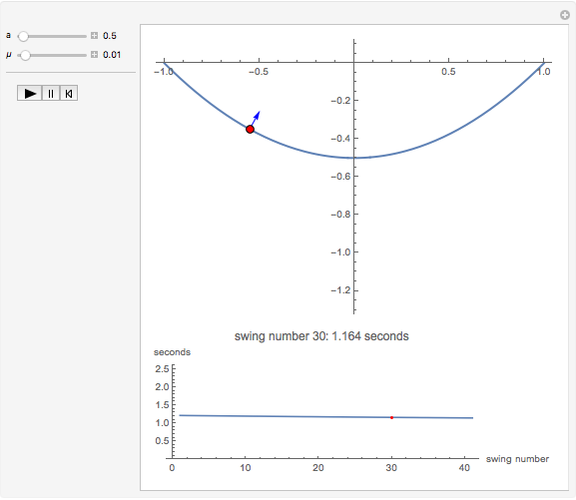
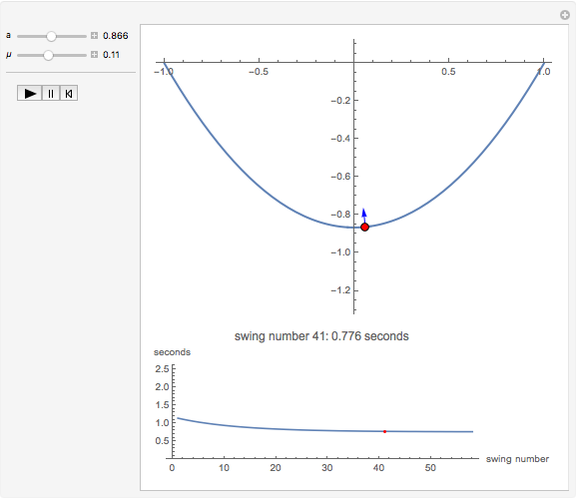
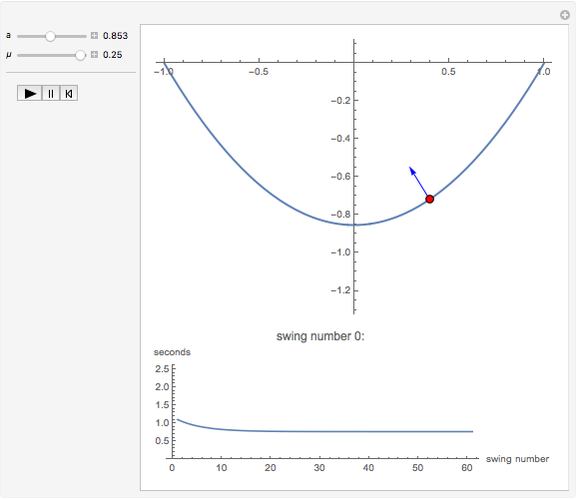
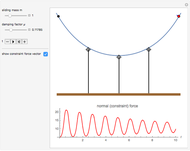
This Demonstration shows an object sliding with damping on a parabolic track with equation 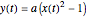. It explores the effect of the damping coefficient and the parameter on the swing period of the object and the constraining force that keeps it on the track.

Contributed by: Erik Mahieu (November 2013)
With additional contributions by: Franz Brandhuber
Open content licensed under CC BY-NC-SA

Snapshots

Details

This Demonstration was inspired by a question in the Wolfram Community site, "Simulating Mechanics of a Cylinder Rolling on a Parabola".

Lagrangian mechanics can be used to derive the equations of motion [1]. The potential energy and kinetic energy are repectively

,

,

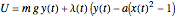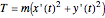where 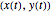is the position of the object at time , 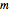is the mass of the object, 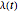is the Lagrange multiplier, and is the damping coefficient.

This gives the equations of motion:

,

,

.

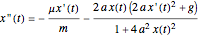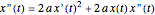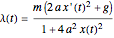Reference

[1] S. Timoshenko and D. H. Young, Advanced Dynamics Chapter III, p. 281, Lagrangian Equations for Impulsive Forces.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send