Spherical Triangle Solutions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
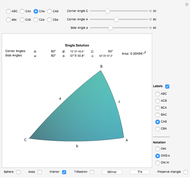
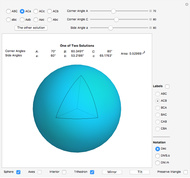
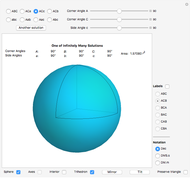
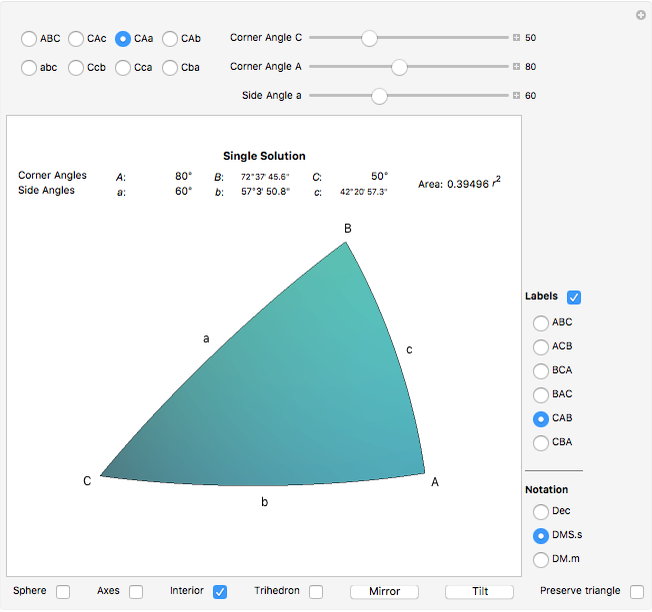
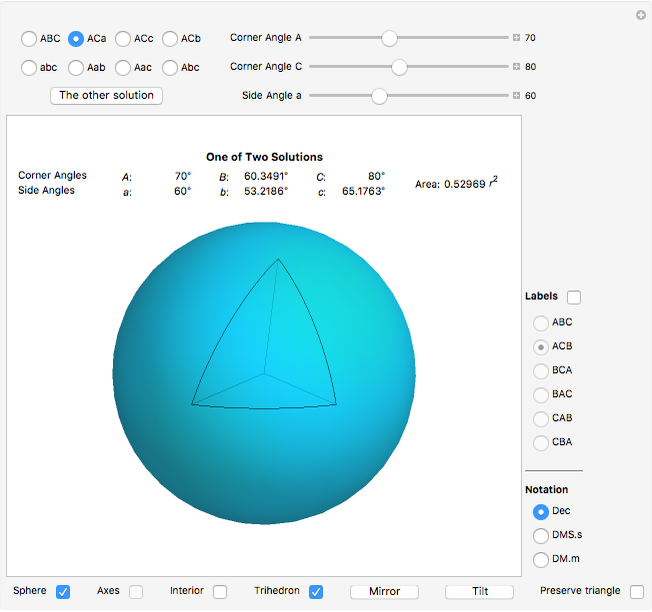
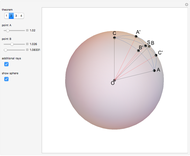
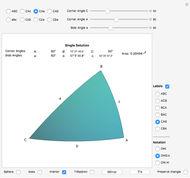
This Demonstration solves and visualizes a spherical triangle, when angular values for three of its six parts are known. If more than one solution exists, alternative solutions are also calculated.
[more]
Contributed by: Hans Milton (May 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
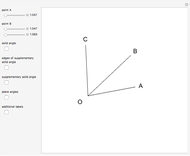
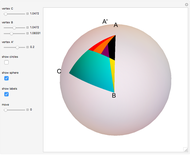
A spherical triangle is a figure on the surface of a sphere, consisting of three arcs of great circles. The shape is fully described by six values: the length of the three sides (the arcs) and the angles between sides taken at the corners. If the side lengths are given in angular measure, the shape description becomes independent of the sphere's radius. This Demonstration solves the unknown three values when the other three are known.
Each side arc defines a plane, which also contains the sphere center. The corner angles are equal to the angles between these planes. The angle between two planes is called a dihedral angle.
There are several conventions for labeling corners, sides, and their angles. Here the corner angles are labeled with capital letters 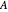 ,
, 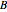 , and
, and 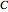 . The angles of opposite sides are labeled
. The angles of opposite sides are labeled  ,
,  , and
, and  .
.
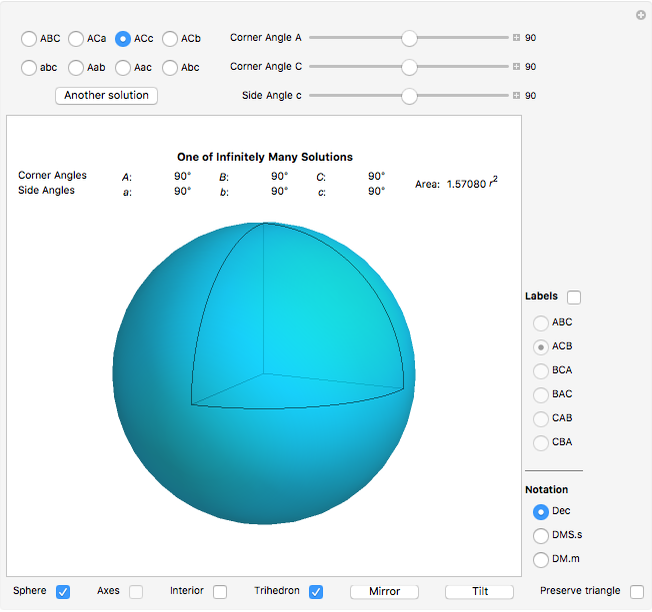
Given three corner or side angles, a solution may or may not exist. If a solution exists it may not be unique. The number of solutions, if any, is either one, two, or infinitely many.
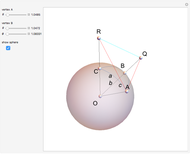
Closely associated with each spherical triangle is its trihedron. In this context it is the triple of lines from the sphere's center to the triangle corners. In other words, the trihedron is the set of position vectors of the corners, with the origin at the sphere's center. An alternative definition of the trihedron also includes the three faces bounded by the lines and triangle sides. The Demonstration visualizes both definitions.
The area of the interior of the triangle can be calculated from the corner angles: 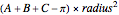 , where the angles are expressed in radians.
, where the angles are expressed in radians.
The most common conventions restrict a spherical triangle to have all corners and sides less than 180°. In contrast this Demonstration allows angles up to and including 180°. Thereby a spherical triangle can take the shape of a spherical lune.
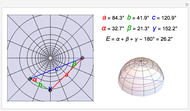
Due to its applications in astronomy and navigation, angles in a spherical triangle may often be expressed in sexagesimal notation. This Demonstration allows for both decimal and sexagesimal notation. Select notation by checking one of the radio buttons Dec, DMS.s (Degrees, Minutes and Seconds with decimal fraction) and DM.m (Degrees and Minutes with decimal fraction).
To apply this Demonstration to great circle navigation, mentally model the corner 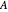 to be located at the north pole and the locations of the corners
to be located at the north pole and the locations of the corners 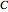 and
and 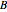 to points of departure and arrival. As the corner angle
to points of departure and arrival. As the corner angle 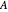 input the difference in longitude between the locations
input the difference in longitude between the locations 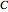 and
and 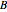 . Input the colatitudes of the locations
. Input the colatitudes of the locations 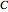 and
and 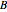 as side angles
as side angles  and
and  , respectively. The solution for side angle a gives the great circle distance in angular measure. To convert to nautical miles, use the fact that
, respectively. The solution for side angle a gives the great circle distance in angular measure. To convert to nautical miles, use the fact that 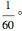 equals one nautical mile (assuming the path traveled is on the surface of a perfectly spherical earth). The course steered at departure is given by the corner angle
equals one nautical mile (assuming the path traveled is on the surface of a perfectly spherical earth). The course steered at departure is given by the corner angle 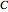 and the course steered at arrival is the supplement to the corner angle
and the course steered at arrival is the supplement to the corner angle 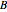 .
.
An example: Lisbon is located at latitude 38°43' 31'' N, and longitude 9°9' W. NewYork is at latitude 40°42' 52'' N, longitude 74° W. The great circle distance between Lisbon and NewYork works out to be 2925 nautical miles.
Permanent Citation