Squares on a Line Segment

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
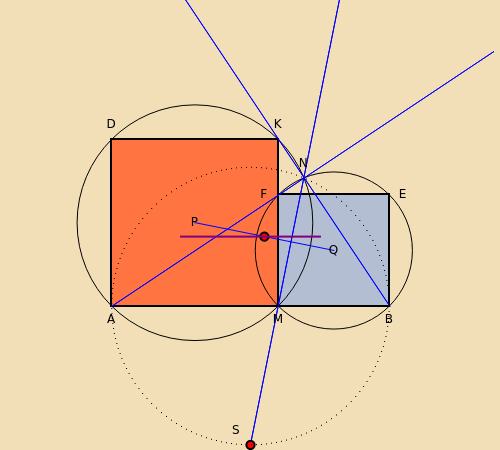
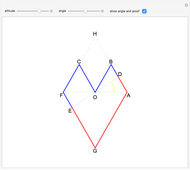
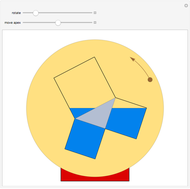
A segment  is given and on it the point
is given and on it the point  . On the same side of
. On the same side of  , the squares
, the squares  and
and  are constructed. The circumcircles of the two squares, whose centers are
are constructed. The circumcircles of the two squares, whose centers are  and
and  , intersect at
, intersect at  and another point
and another point  .
.
Contributed by: Jaime Rangel-Mondragon (July 2013)
Open content licensed under CC BY-NC-SA
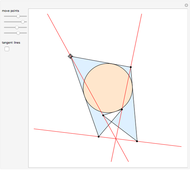
Snapshots
Details
This is the first of a series of Demonstrations dedicated to showcasing a sample of problems posed for the International Mathematical Olympiads (IMO), the most important and prestigious annual mathematical competition for high school students, which began in 1959. (In 1980, financial problems caused no country to volunteer to host it.)
The problems chosen have an intrinsic geometrical appeal and provide an interesting programming challenge, met with the framework provided by Mathematica. The statement of the problems we present follows the original ones, in which the proof of a series of assertions is required.
Our goal is to aid in the visual understanding of the problem and of its assertions. Sometimes a visual hint of the proof itself is provided; for instance, the dotted circle having  as its diameter passes through
as its diameter passes through  and
and  , and the locus of part (c) is indicated in purple. This problem was taken from the first IMO in Bucharest-Brasov, Romania, July 23-31, 1959, problem 5 [1].
, and the locus of part (c) is indicated in purple. This problem was taken from the first IMO in Bucharest-Brasov, Romania, July 23-31, 1959, problem 5 [1].
Reference
[1] D. Djukić, V. Janković, I. Matić, and N. Petrović, The IMO Compendium, 2nd ed., New York: Springer, 2011.
Permanent Citation