Stellar Luminosity

Initializing live version

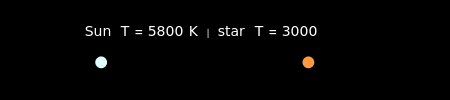
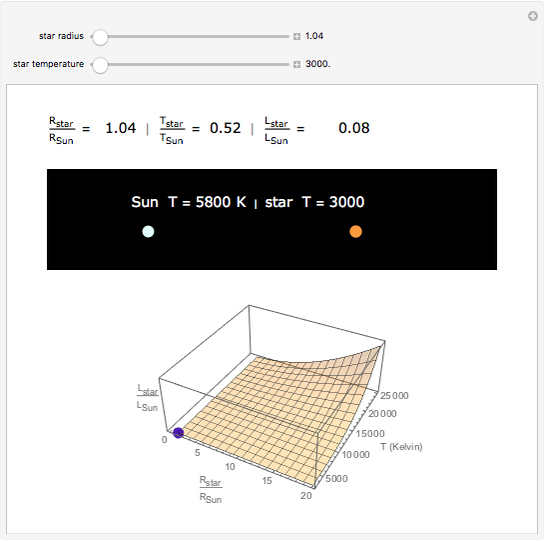
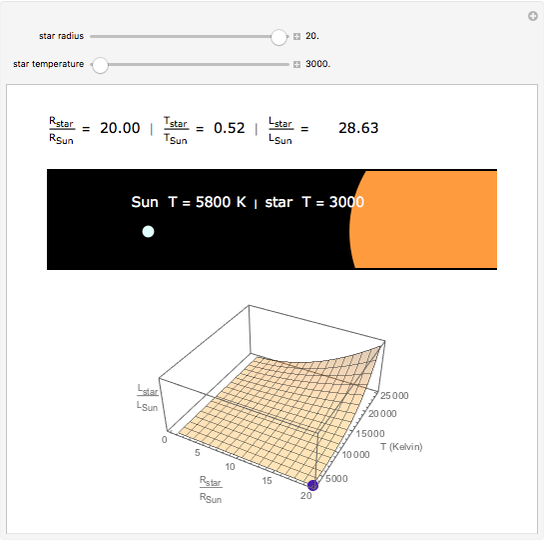
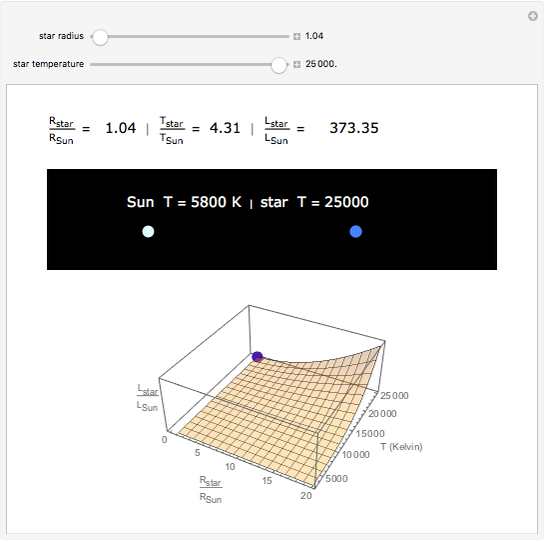
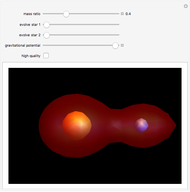
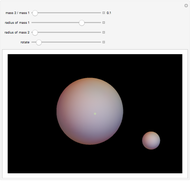
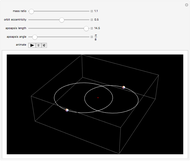
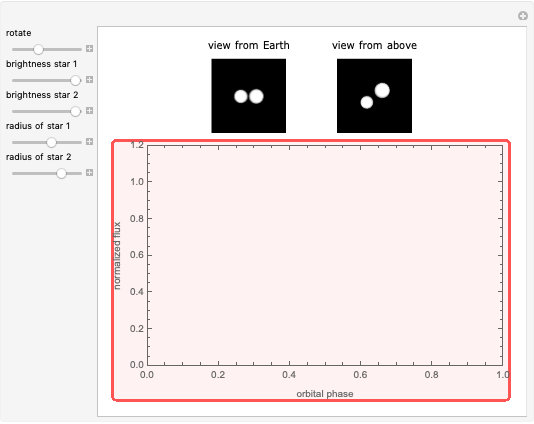
The luminosity, the amount of light emitted by a star, depends on the star's size and temperature.

Contributed by: Jeff Bryant (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

The luminosity of a star is proportional to the surface area times the energy radiated per square meter (σ is the Stefan-Boltzmann constant):

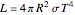
Dividing the expressions for the luminosities of a star and the Sun allows us to compare them:

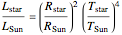
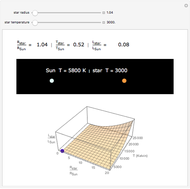
Snapshot 1: A star the same size as the Sun but about half as hot is much less luminous than the Sun.

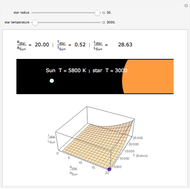
Snapshot 2: A star about half as hot as the Sun but 20 times larger is nearly 29 times more luminous than the Sun.

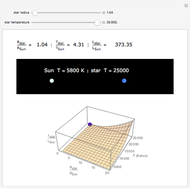
Snapshot 3: A star the same size as the Sun that is about 4 times hotter is over 345 times more luminous than the Sun.

Snapshot 4: A star 20 times the size of the Sun and about 4 times hotter is over 138,000 times more luminous than the Sun.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send