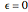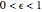The Celestial Two-Body Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
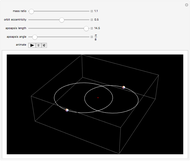
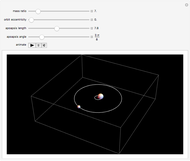
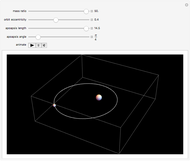
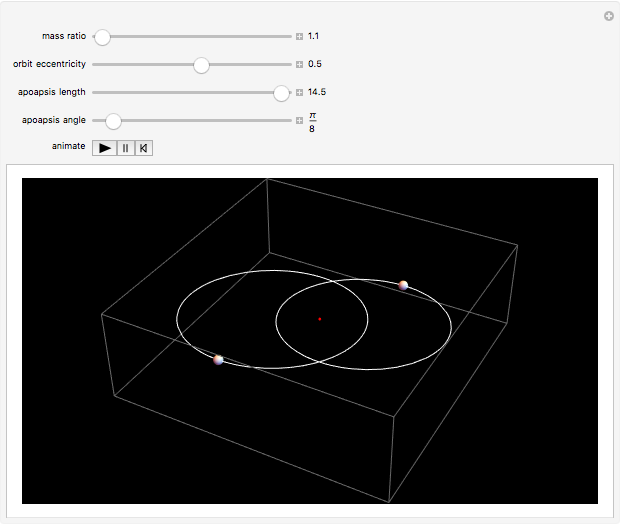
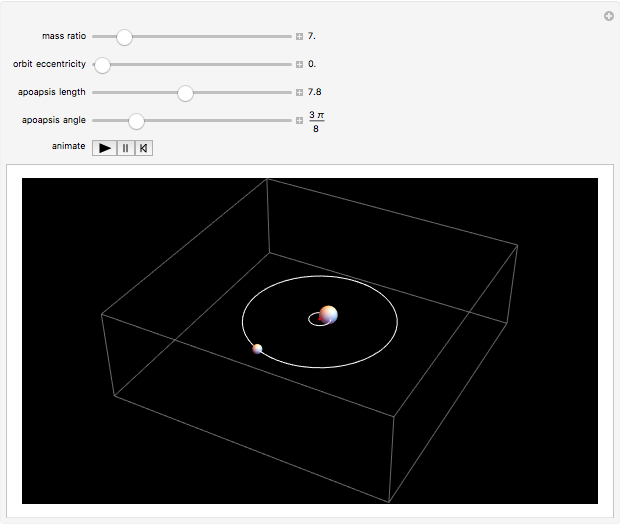
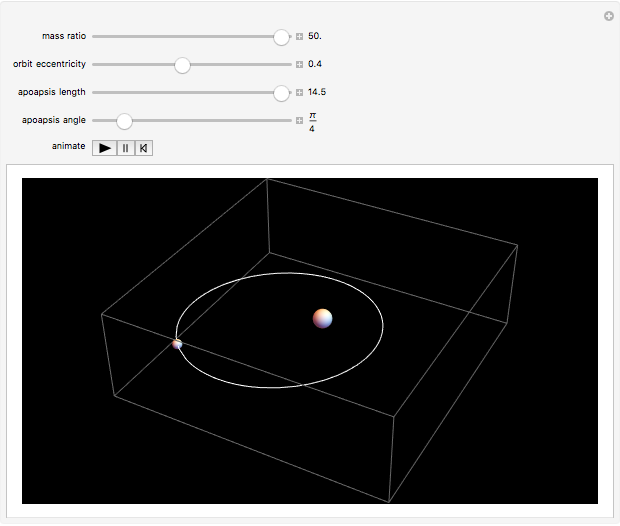
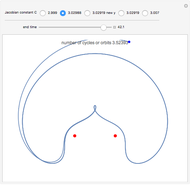
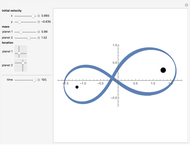
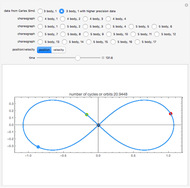
Two celestial bodies interacting gravitationally can establish a stable system in which both trace out elliptical (or possibly circular) orbits about their mutual barycenter (center of mass), marked with a red dot. Each orbit individually follows Kepler's three laws of planetary motion.
[more]
Contributed by: S. M. Blinder (March 2011)
After suggestions by: Jeff Bryant and Ed Pegg Jr
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: the binary or double star 61 Cygni, also known as Bessel's star; the period of rotation is approximately 659 years
Snapshot 2: the dwarf planet Pluto with its companion Charon, with about a seventh of the mass; the barycenter of the system orbits the Sun with a period of 248.5 years
Snapshot 3: a star with a planet 1/50 of its mass; the star's wobbling motion is apparent
Snapshot 4: approximate representation of a comet in orbit around the Sun; the eccentricity approaches 1
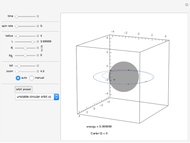
Snapshot 5: the lowest Bohr orbit for a muonic atom: a negative muon 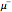 orbiting a proton; the Bohr radius is about 1/207 that of a hydrogen atom
orbiting a proton; the Bohr radius is about 1/207 that of a hydrogen atom
Permanent Citation