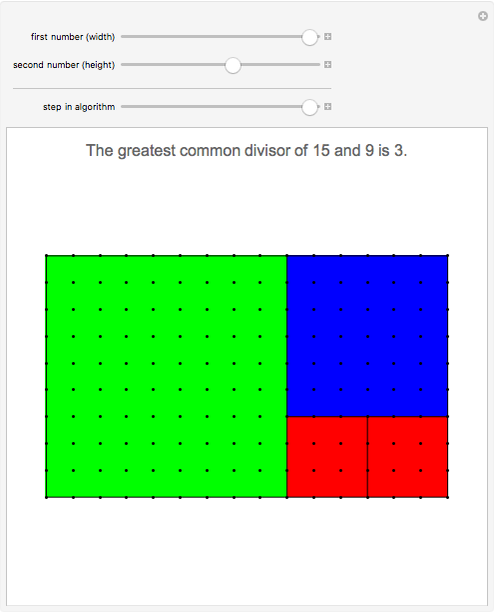
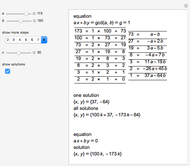
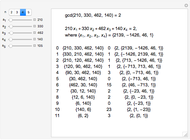
The Euclidean Algorithm and Simple Continued Fractions

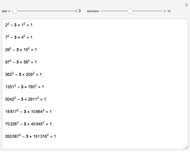
The simple continued fraction expansion of a real number is finite if and only if is rational. The process of finding the simple continued fraction expansion of a rational number is in principle identical to the process of applying the Euclidean algorithm to its numerator and denominator. For example,

.

The underlying Mathematica program is an adaptation of the one used in The Wolfram Demonstration Projects Euclidean Algorithm Steps by Michael Trott and Extended Euclidean Algorithm by Štefan Porubský.

(The author was supported by project 1ET200300529 of the program Information Society of the National Research Program of the Czech Republic and by the Institutional Research Plan AV0Z10300504; the Demonstration was submitted 2008-06-04, revised 2010-03-13.)