Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

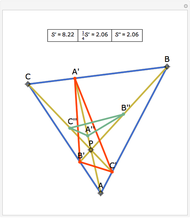
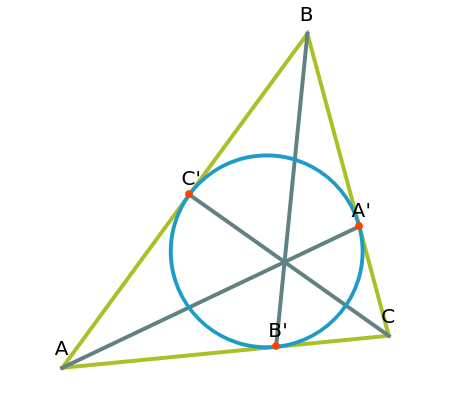The Gergonne Point

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

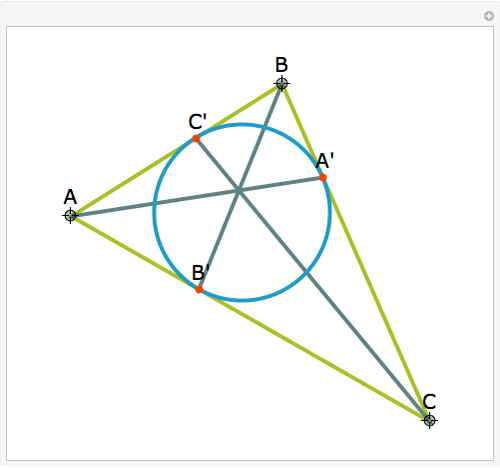
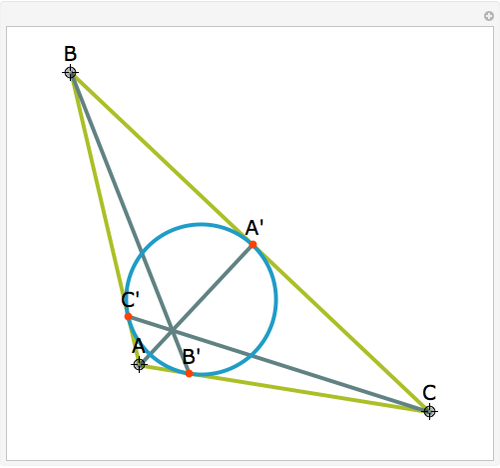
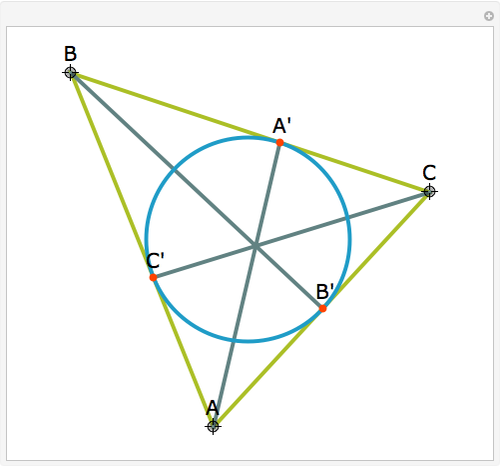
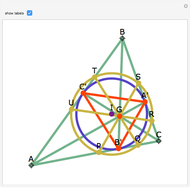
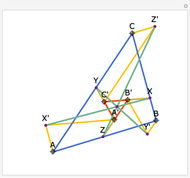
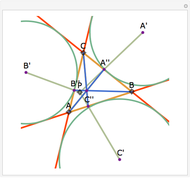
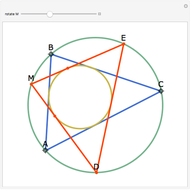
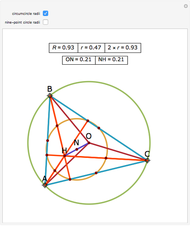
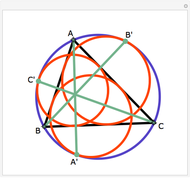
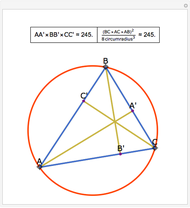
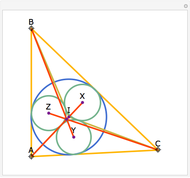
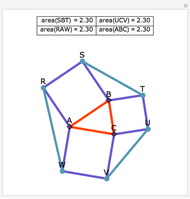
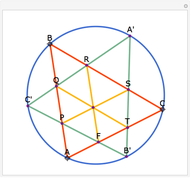
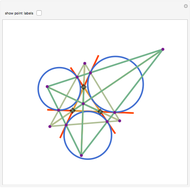
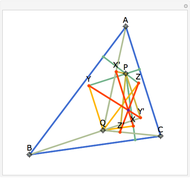
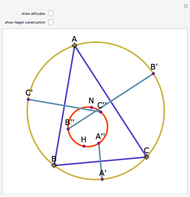
Let ABC be a triangle. Let A', B', and C' be the points of contact of ABC with the incircle opposite A, B, and C, respectively. Then AA', BB', and CC' are concurrent at the Gergonne point.

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

Details

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send