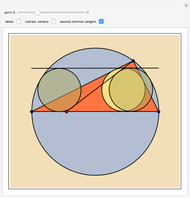
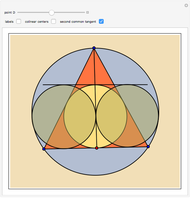
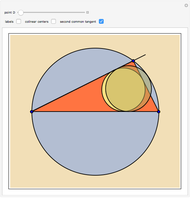
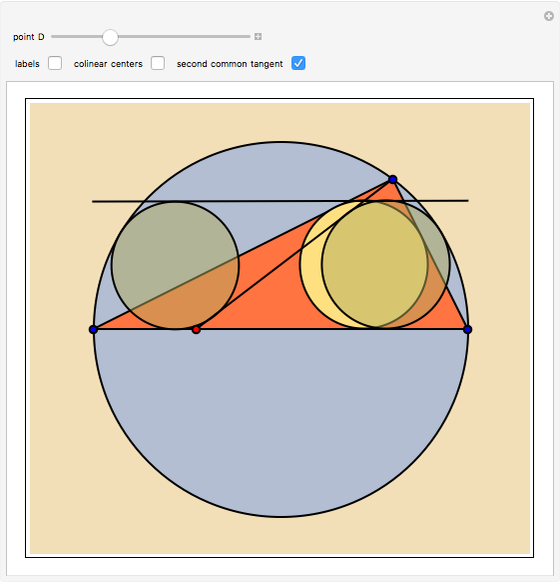
Three Circles with Two Common Tangents
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
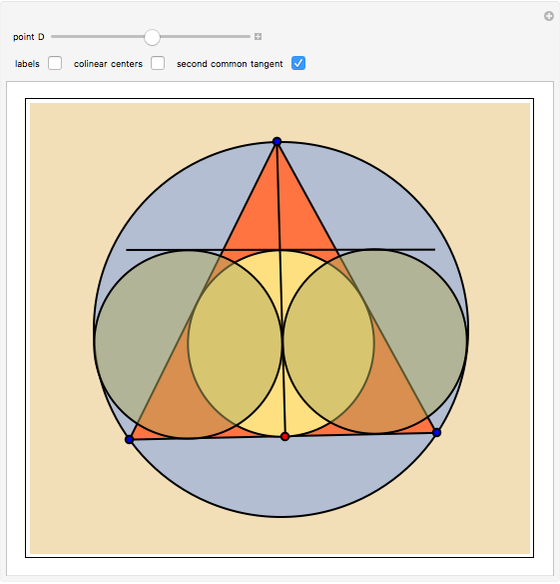
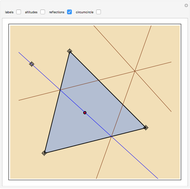
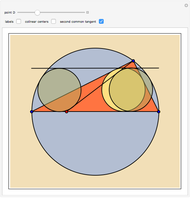
Let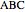 
be a triangle circumscribed by the circle 
. Let 
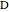be a point on 
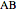; form the line 
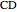. Consider three other circles 
, 
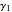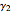, and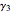 
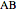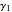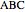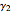with the common tangent , with inscribed in the triangle , and and 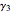tangent to both the segment 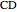and . Prove that 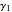, , 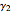and 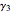have two common tangents.
Contributed by: Jaime Rangel-Mondragón (July 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
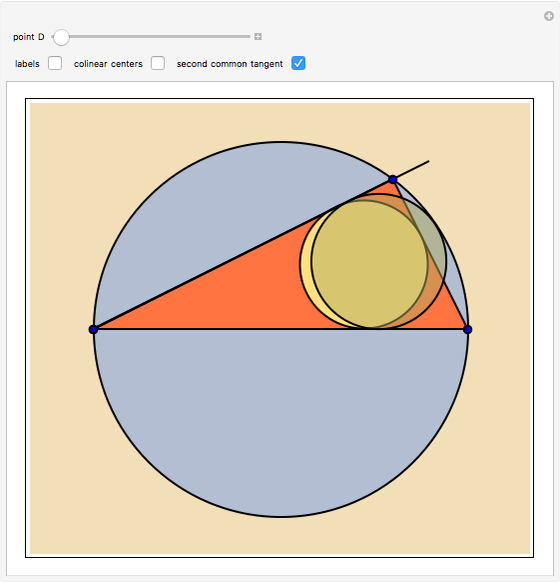
The statement holds for arbitrary points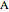 
, 
, 
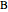on . Moreover, the statement holds for an arbitrary point 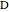on 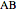. You can drag the vertices A, B and C and change the position of 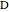using a slider. This is problem 4 from the eleventh International Mathematical Olympiad (IMO) held in Bucharest, Romania, July 5–20, 1969.
Reference
[1] D. Djukić, V. Janković, I. Matić, and N. Petrović, The IMO Compendium: A Collection of Problems Suggested for the International Mathematical Olympiads, 1959–2009, 2nd ed., New York: Springer, 2011.
Permanent Citation
Three Equal Segments from the Altitudes of a Triangle
Jaime Rangel-Mondragon
Circumcircles of Two Midpoints and an Altitude
Jaime Rangel-Mondragon
Reflections of a Line through the Orthocenter in the Sides of an Acute Triangle
Jaime Rangel-Mondragon
Bisecting the Area and Perimeter of a Triangle
Jaime Rangel-Mondragon
Squares on a Line Segment
Jaime Rangel-Mondragon
Making the Three Areas Defined by Congruent Overlapping Circles Equal
Kenneth E. Caviness and Eugene Stewart
Two-by-Two Linear Systems Problem Generator
Bruce Torrence
Halving the Perimeter of a Zigzag Polygon
Izidor Hafner
A Triangle Inequality Involving the Altitudes, Semiperimeter, Inradius, and Circumradius
Jay Warendorff
Construction for Three Vectors with Sum Zero
Izidor Hafner
