,

with the Hamiltonian

expressed in atomic units . For S-states, including the ground state, the wavefunction depends on just three variables: , , and . Hylleraas used these alternative variables: , , and . Consider simple trial functions of the form . We need the combination in order that is an even function of , thus a symmetric function with respect to the interchange of and .

According to the variational principle, the ground-state energy can be approximated by , where

.

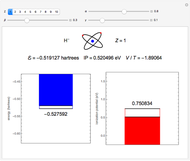
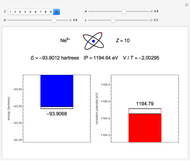
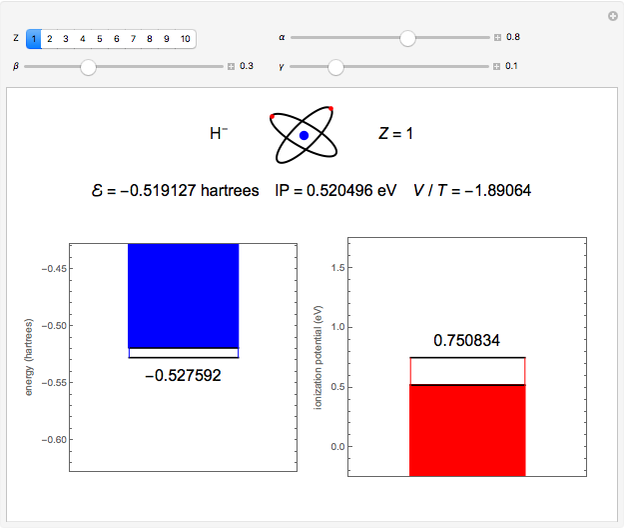
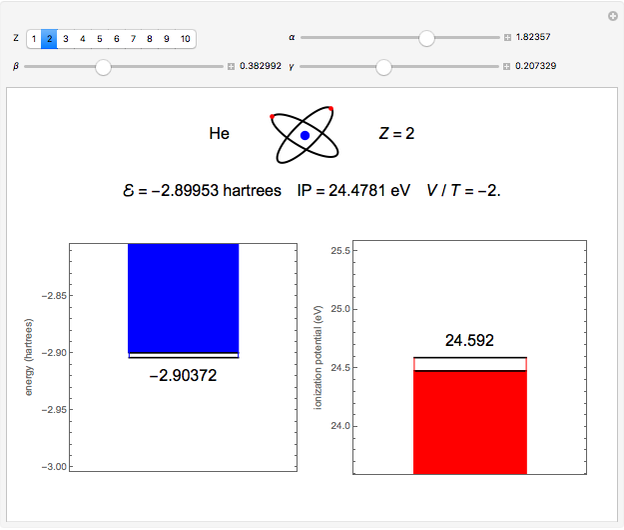
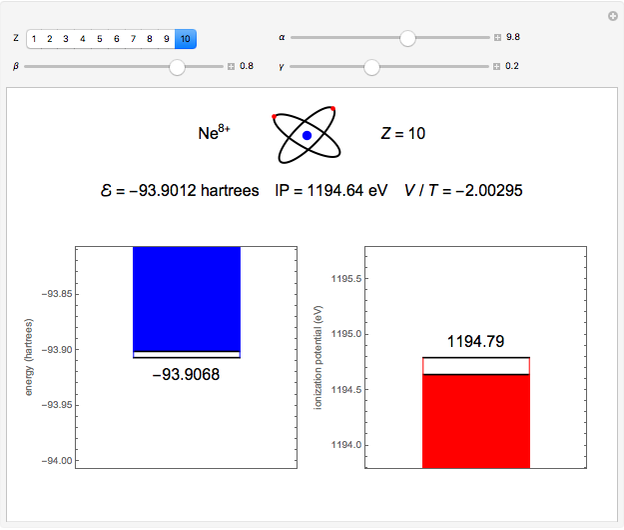
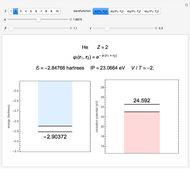
The parameters , , and are then selected such that takes a minimum value. This is always an upper bound on the exact ground-state energy . To run this Demonstration, choose a value of corresponding to one of the two-electron atoms or ions. Then, vary the sliders determining various combinations of α, β, and γ. The ionization potential () is the energy to remove one electron, which leaves the atom in the one-electron energy state . The is expressed in (). As the blue and red areas become larger, exact values of the energy and ionization potential are being approached more closely. Also shown is the ratio of expectation values of potential and kinetic energies, . By the virial theorem for Coulombic systems, this ratio should equal . This value would be obtained by the exact solution of the Schrödinger equation, but also for an approximate solution with optimally chosen variational parameters.

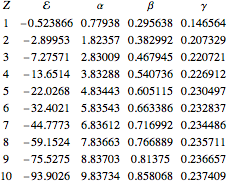
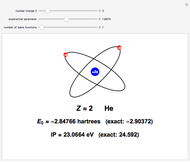
If you want to look at the answers, the optimal values of , , and are tabulated in the Details section.