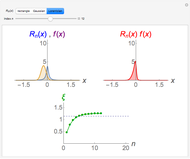
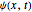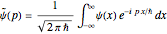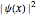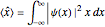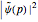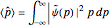Time-Dependent Superposition of Harmonic Oscillator Eigenstates
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
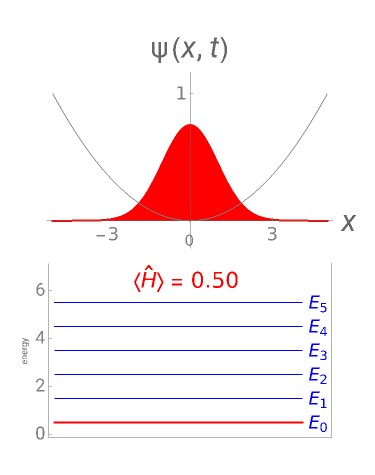
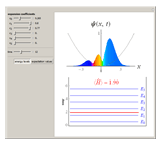
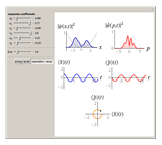
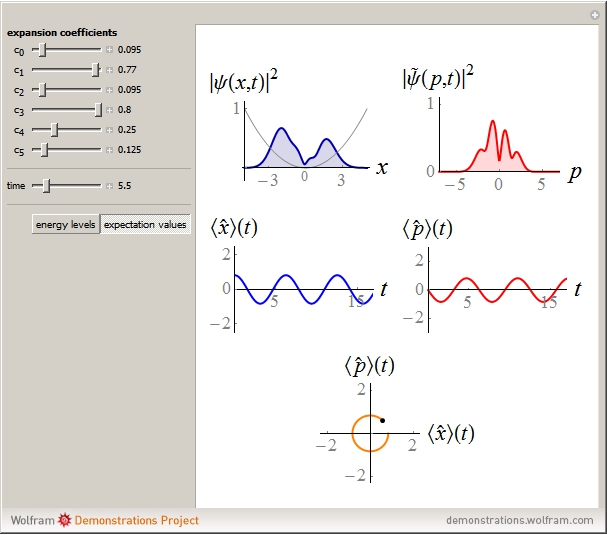
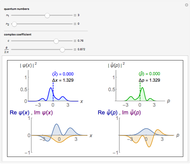
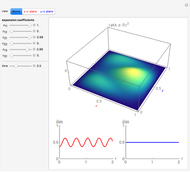
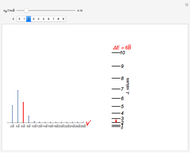
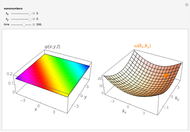
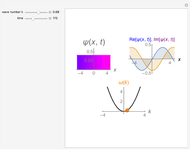
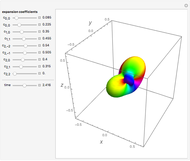
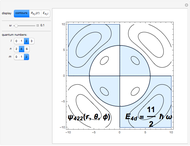
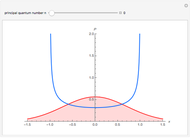
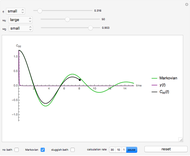
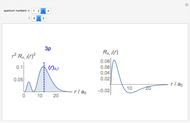
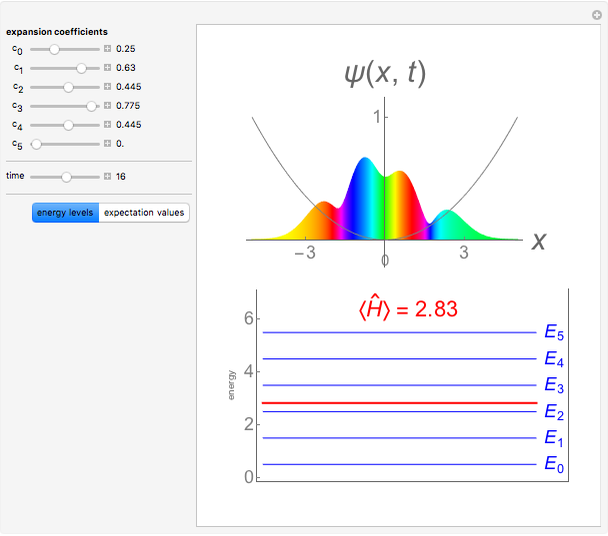
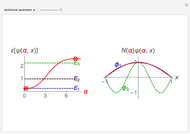
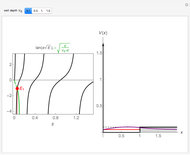
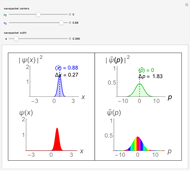
Consider a time-dependent superposition of quantum harmonic oscillator eigenstates, 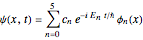 , where the eigenfunctions and eigenvalues are given by
, where the eigenfunctions and eigenvalues are given by 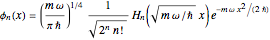 and
and 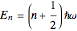 , respectively. Here
, respectively. Here 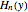 is the
is the 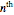 Hermite polynomial. The Hamiltonian for this system is
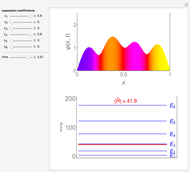
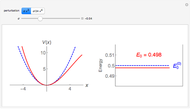
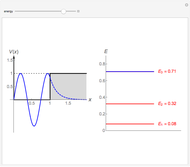
Hermite polynomial. The Hamiltonian for this system is 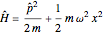 and its energy expectation value is given by
and its energy expectation value is given by 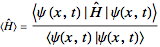 .
.
Contributed by: Porscha McRobbie and Eitan Geva (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation