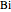Transient Cooling of a Sphere

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
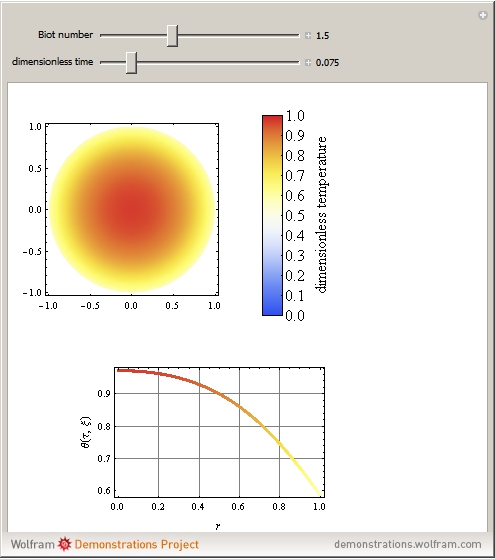
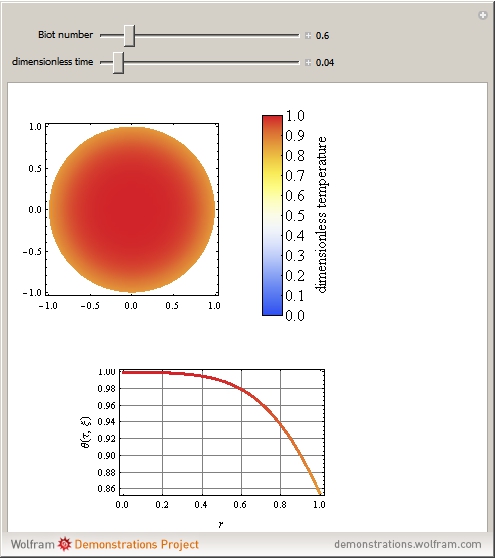
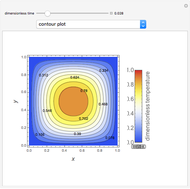
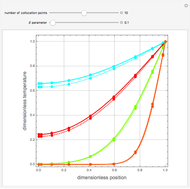
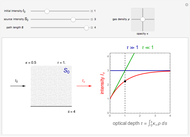
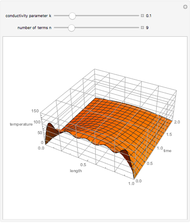
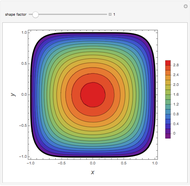
This Demonstration shows transient heat conduction in a sphere of radius 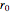 . At time
. At time 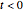 , the sphere is held at a uniform temperature
, the sphere is held at a uniform temperature 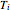 . At time
. At time  , the sphere is immersed in a well-mixed cooling bath at temperature
, the sphere is immersed in a well-mixed cooling bath at temperature 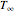 . The sphere loses heat from its surface according to Newton's law of cooling:
. The sphere loses heat from its surface according to Newton's law of cooling: 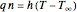 , where
, where  is a heat transfer coefficient. Assume that at any time in the cooling process, the temperature distribution within the sphere depends solely on the radial coordinate; in a spherical coordinate system, the temperature is symmetric with respect to the azimuthal and polar angles.
is a heat transfer coefficient. Assume that at any time in the cooling process, the temperature distribution within the sphere depends solely on the radial coordinate; in a spherical coordinate system, the temperature is symmetric with respect to the azimuthal and polar angles.
Contributed by: Housam Binous and Brian G. Higgins (January 2013)
Open content licensed under CC BY-NC-SA
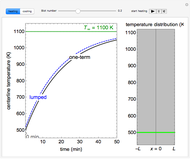
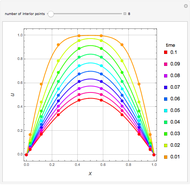
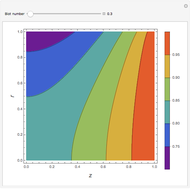
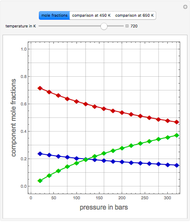
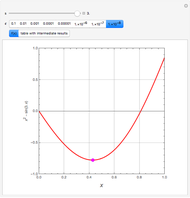
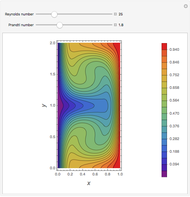
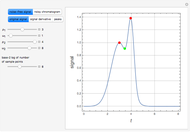
Snapshots
Details
The mathematical problem involved is:
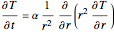 for
for 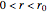
subject to the following initial conditions (IC) and boundary conditions (BC)
IC: 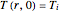 ,
,
BC 1: 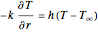 for
for 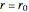 ,
,
BC 2: 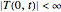 .
.
The material parameters of the sphere that affect heat transfer are  , the thermal diffusivity
, the thermal diffusivity 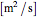 and
and  , the thermal conductivity
, the thermal conductivity 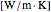 .
.
The heat transfer coefficient  for the sphere/bath system
for the sphere/bath system 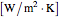 accounts for the resistance associated with heat loss from the sphere to the fluid and is a function of the local mixing properties of the bath as well as the fluid thermal properties.
accounts for the resistance associated with heat loss from the sphere to the fluid and is a function of the local mixing properties of the bath as well as the fluid thermal properties.
To solve this problem it is convenient to introduce the following dimensionless variables:
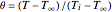 ,
, 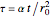 , and
, and 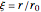 .
.
Thus the PDE and IC/BCs become:
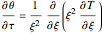 for
for 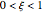 ,
,
IC : 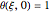 ,
,
BC1: 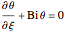 for
for  ,
,
BC2: 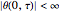 ,
,
where 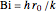 is a dimensionless quantity called the Biot number, a measure of the relative importance of resistance, heat conduction within the sphere, and resistance of heat loss to the surrounding fluid.
is a dimensionless quantity called the Biot number, a measure of the relative importance of resistance, heat conduction within the sphere, and resistance of heat loss to the surrounding fluid.
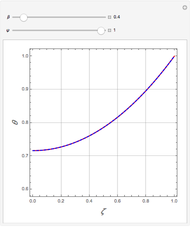
Using the method of separation of variables, you obtain the following solution:
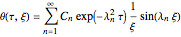 ,
,
where 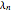 are the roots of
are the roots of 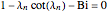 and
and 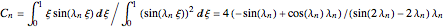 .
.
Permanent Citation