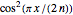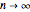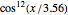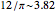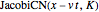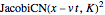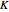Travelling Pulses (Wave Packets)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
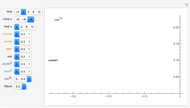
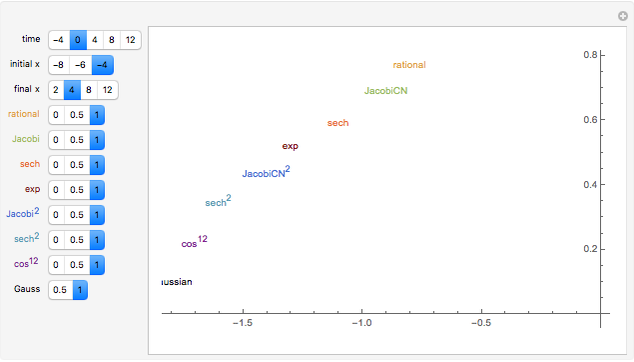
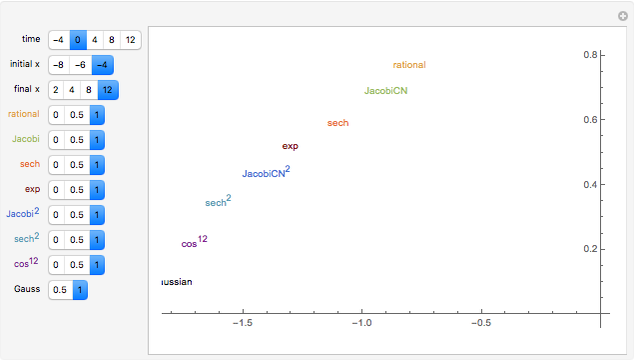
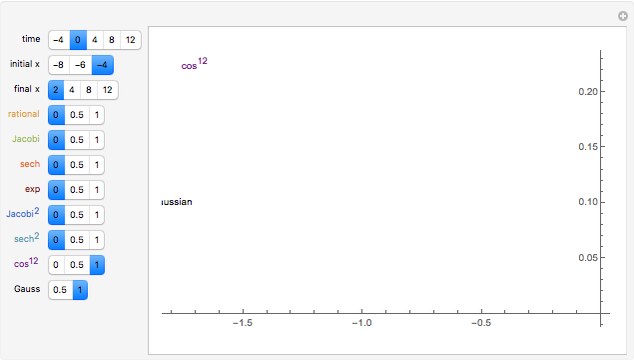
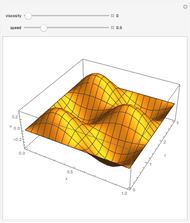
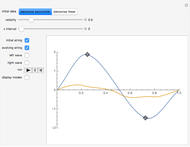
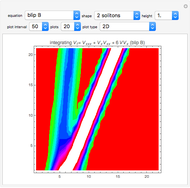
Various travelling pulses (or wave packets) are displayed; they have similar central shapes but different decay rates. They are given different velocities, so they separate when the time,  , is not zero. The Gaussian curve (with velocity zero) is always shown; the amplitudes of the others can be 0, .5, or 1. The rising arm is labelled if the amplitude is 1.
, is not zero. The Gaussian curve (with velocity zero) is always shown; the amplitudes of the others can be 0, .5, or 1. The rising arm is labelled if the amplitude is 1.
Contributed by: Roger Beresford (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
These pulses are solutions to nonlinear partial differential equations that will be developed in other Demonstrations. The 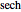 and
and 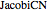 pulses are constant amplitude solitonic solutions to the Modified‐Korteweg–deVries equation;
pulses are constant amplitude solitonic solutions to the Modified‐Korteweg–deVries equation; 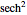 and
and 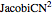 are solutions to the original Korteweg–deVries equation. These equations include nonlinearities that cancel the dispersive effect of the change of velocity with frequency (so the pulses do not become lower and wider with time). Different amplitude solitons have different velocities, "passing through" each other with a "change of phase" (not shown in this Demonstration). The Schrödinger equation has Gaussian wave packet solutions that do become lower and wider as time passes—it describes "information about particles". Presumably there is an undiscovered equation that describes sets of stable particles as multi-dimensional wave packets.
are solutions to the original Korteweg–deVries equation. These equations include nonlinearities that cancel the dispersive effect of the change of velocity with frequency (so the pulses do not become lower and wider with time). Different amplitude solitons have different velocities, "passing through" each other with a "change of phase" (not shown in this Demonstration). The Schrödinger equation has Gaussian wave packet solutions that do become lower and wider as time passes—it describes "information about particles". Presumably there is an undiscovered equation that describes sets of stable particles as multi-dimensional wave packets.
Permanent Citation