Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Varying Period of a Damped Pendulum

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

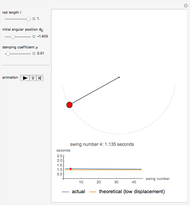
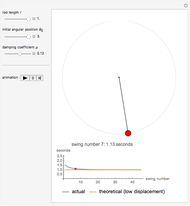
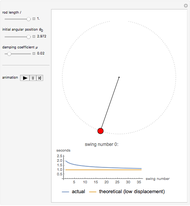
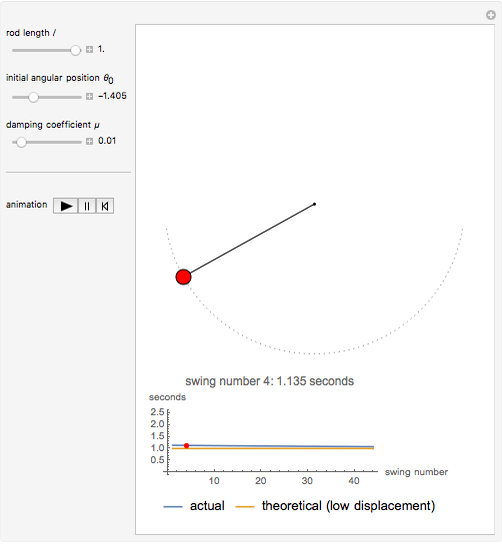
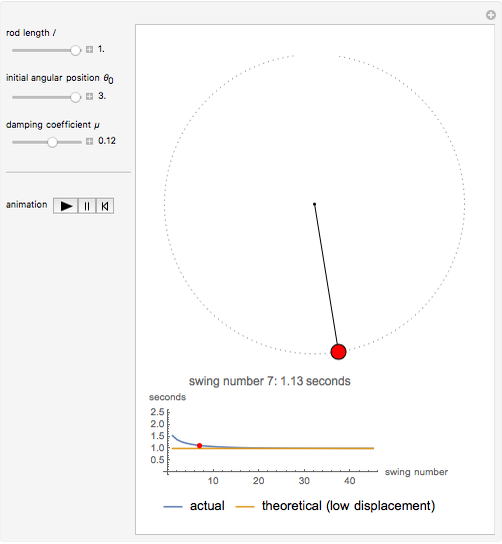
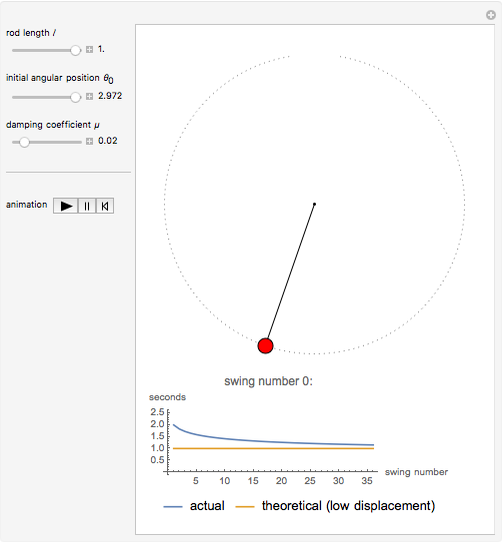
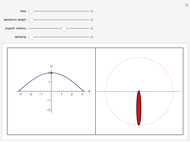
This Demonstration explores the effect that the rod length, damping coefficient, and initial position have on the period of a damped pendulum.

[more]

Mathematica's built-in function WhenEvent, triggered whenever the bob crosses the vertical, detects the time of successive swings of the pendulum.

The actual swing period can be compared to the theoretical one that is valid for small initial angles only, , where is time and is the acceleration due to gravity.

[less]

Contributed by: Erik Mahieu (November 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The well-known equation of motion of the damped pendulum is used: 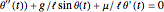, where is the angle from the vertical, is time, is the acceleration due to gravity, is the length of the pendulum, and is the damping factor.

During the solution of the differential equation, WhenEvent is triggered by the event 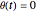and the resulting action collects the time at each crossing.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send