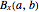Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Visualizing the Exact Median Rank

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

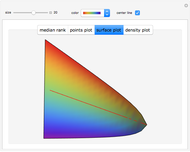
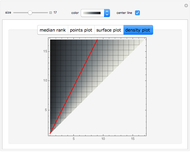
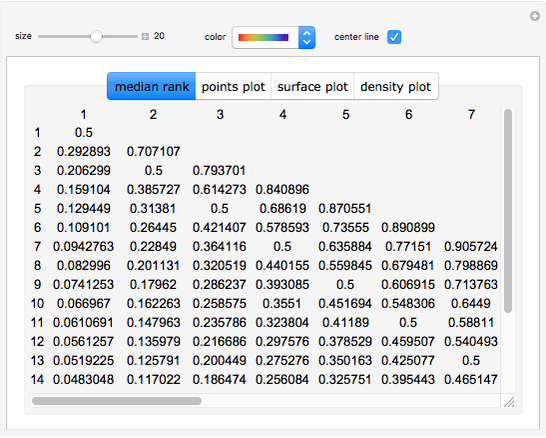
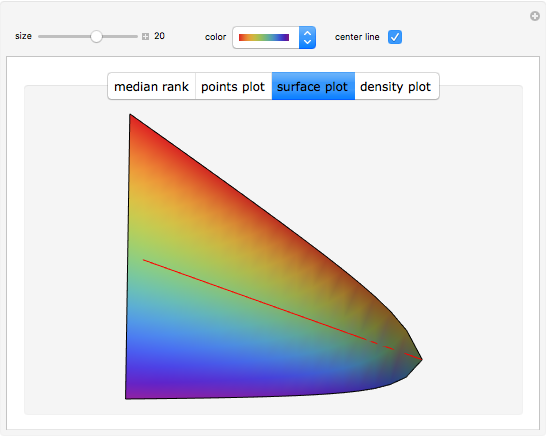
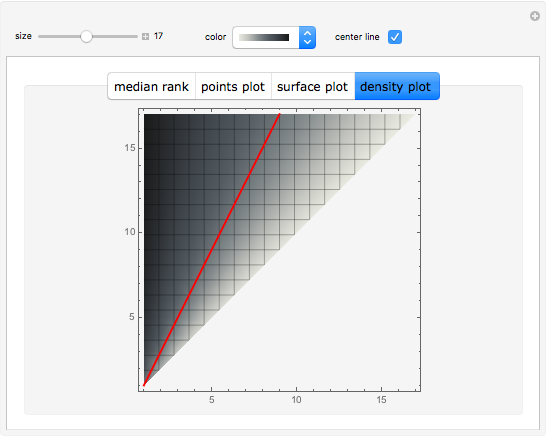
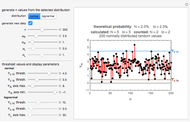
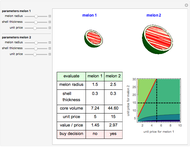
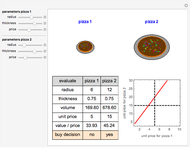
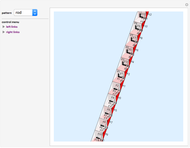
The median rank function 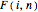is used to estimate the cumulative probability of failure of the 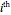of identically stressed samples. There are several simple formulas proposed by Weibull and others [1] that give approximate values for the median rank.

[more]

The exact median rank function is related to the incomplete beta function , which is hard to calculate. Jacquelin [2] recommends an algorithm based on the Newton-Raphson method.

This Demonstration presents the exact median rank using Jacquelin's method and plots it in different ways.

[less]

Contributed by: Frederick Wu (March 2011)
Based on work by: Jean Jacquelin
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference:

[1] W. Weibull, Fatigue Testing and Analysis of Results, New York: Pergamon Press, 1961 pp. 193–199.

[2] J. Jacquelin, "A Reliable Algorithm for the Exact Median Rank Function," IEEE Transactions on Electrical Insulation, 28(2), 1993 pp. 168–171.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send