Wave Functions of Identical Particles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
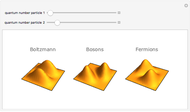
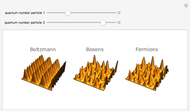
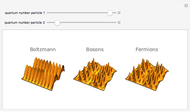
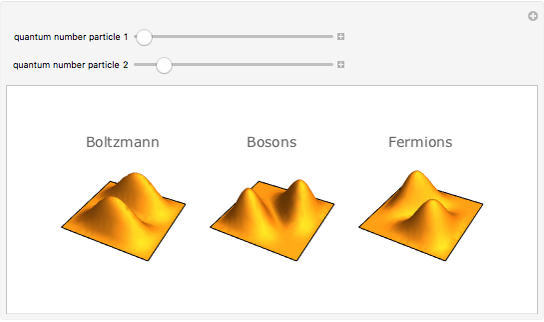
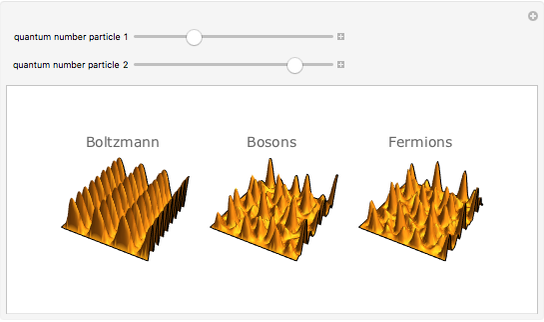
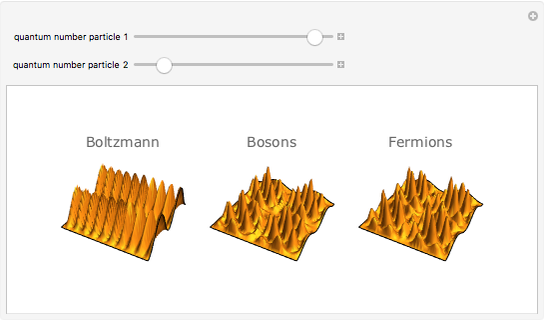
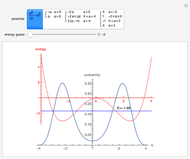
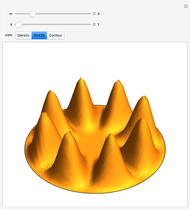
Quantum mechanical probability density for two particles in a 1D well with infinite walls.
Contributed by: Michael Trott (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In classical statistical mechanics, identical particles are considered indistinguishable from each other (the Boltzmann‐Gibbs case). Quantum mechanically, an elementary particle (meaning an irreducible finite-dimensional representation of the Poincaré group) is either a boson or a fermion, according to whether its spin (the Casimir operator of the Poincaré group) is an integer or a half-integer. Bosons and fermions cannot mix (superselection rule); wave functions representing identical bosons [fermions] must be fully symmetric [antisymmetric]. These symmetry requirements make an imprint on the probability distributions of particle groups. Statistically, bosons tend to be bunched together and fermions tend to keep away from each other, forming correlation holes. This Demonstration shows the two-particle probability distributions for the simplest possible case--particles in a square well.
Permanent Citation
"Wave Functions of Identical Particles"
http://demonstrations.wolfram.com/WaveFunctionsOfIdenticalParticles/
Wolfram Demonstrations Project
Published: March 7 2011