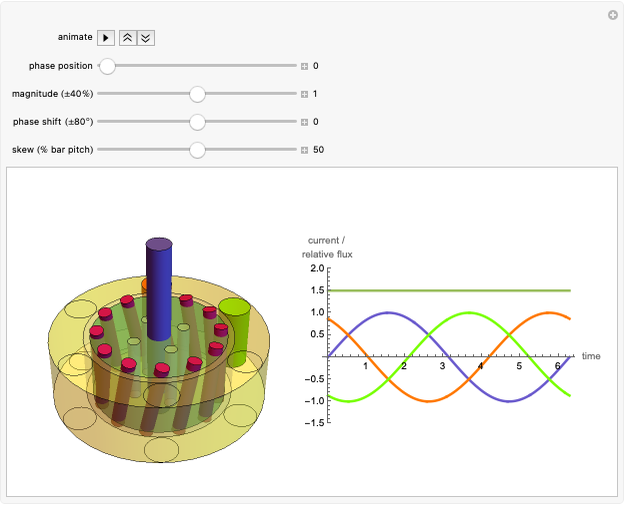
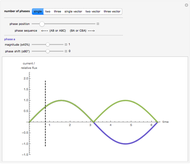
AC Rotating Magnetic Field Principle

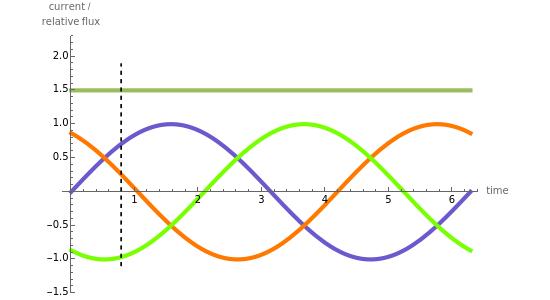
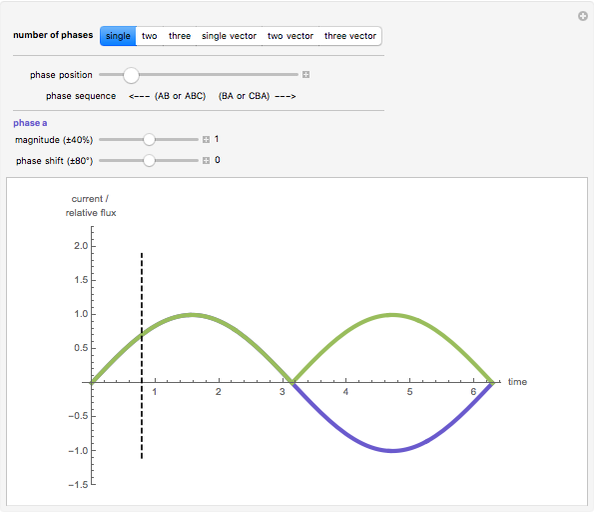
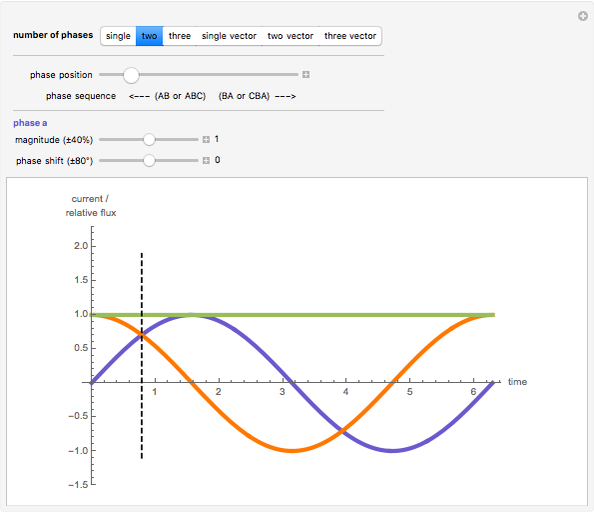
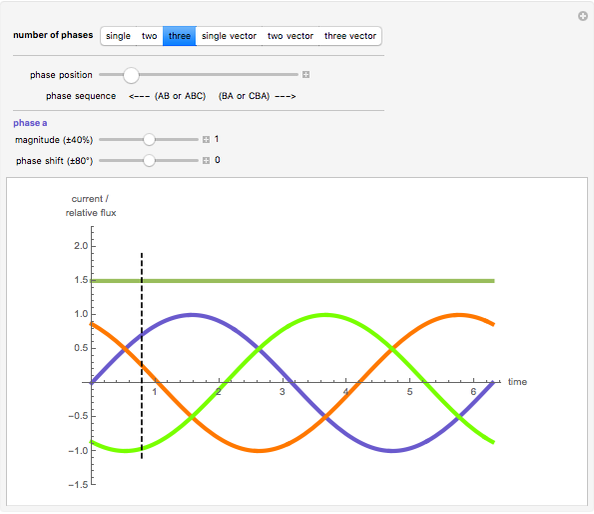
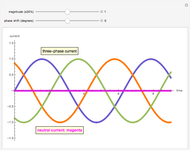
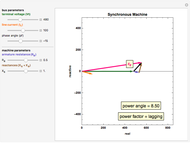
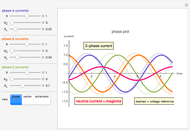
The dark green plot in the phase diagrams is the resulting relative magnitude of the magnetic field created by the sine wave source currents. Within the vector plots, the red ball represents the time position and the dashed black vector is the resultant vector when the phases are added together.

The consistent magnitude of the magnetic field is apparent when viewing poly-phase systems and varies greatly with a single-phase source. Adjusting the magnitude or phase displacement of one of the phases in any of the systems illustrates the resulting change in magnetic field magnitude. Any inconsistency in the magnitude of the magnetic field results in a change in torque development and possibly speed variation of an electrical machine.

Phase can be adjusted in magnitude and phase relationship to the other phases. This allows for demonstrating the effects of high or low current on a leg due to voltage variations. The phase adjustment allows for illustration of the effects of a power factor change on one phase only.