Arbitrary Curves of Constant Width

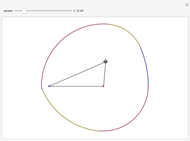
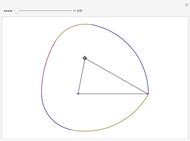
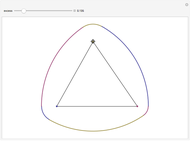
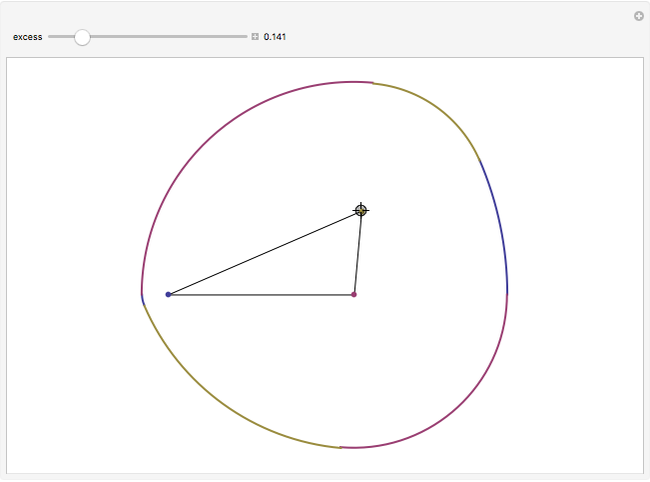
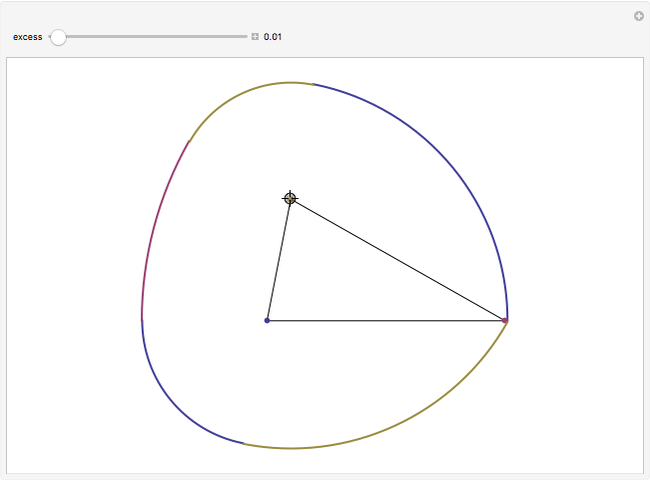
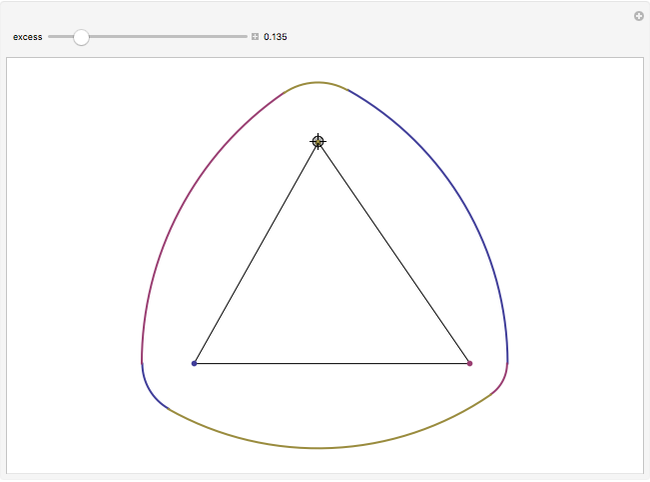
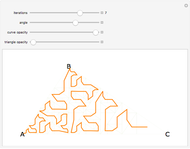
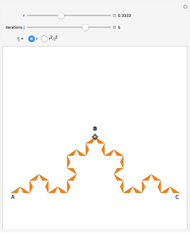
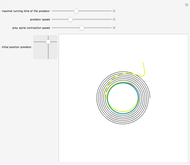
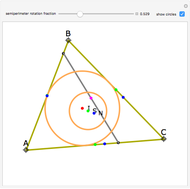
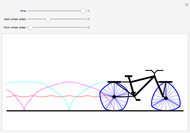
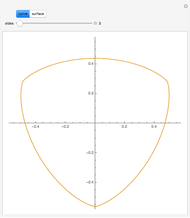
Both the circle and the Reuleaux triangle are examples of curves of constant width. Such curves, if fitted into a square, can rotate in constant contact with all four sides. Any triangle can serve as a template for a curve of constant width by putting three pairs of arcs of circles around it, centered at each of the three vertices, as shown by this Demonstration.