Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Curves and Surfaces of Constant Width

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

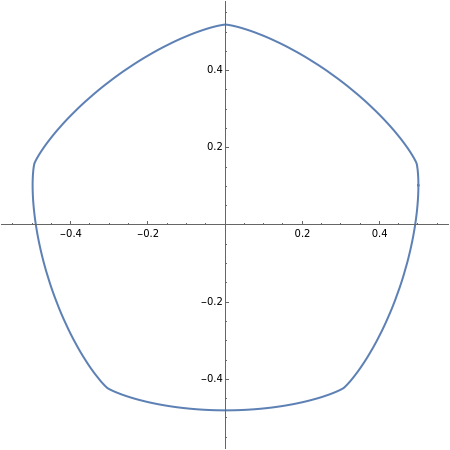
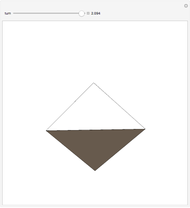
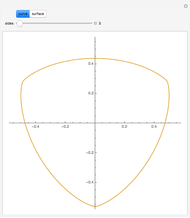
Curves of constant width are useful for noncircular coins. As the number of sides increases, these curves quickly become more like disks and less like Reuleaux triangles. The curves here are defined using a simple support function: for an odd integer, .

[more]

To preserve convexity, is needed. Support functions have a central role in the definition of sets of constant width; for example, in the Eggleston (1952) proof of the Blaschke–Lebesgue (1914) theorem, the Reuleaux triangle is the planar set of constant width of minimal area.

[less]

Contributed by: Ian Calvert (April 2012)
Case for surfaces by: Izidor Hafner
Open content licensed under CC BY-NC-SA

Snapshots

Details

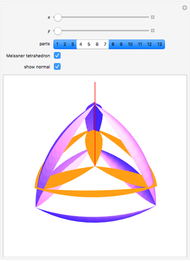
Rotating a curve of constant width about an axis of symmetry creates a surface of constant width [1, p. 196], but there are other kinds of surfaces of constant width. There are curves of constant width without an axis of symmetry [2].

References

[1] J. Bryant and C. Sangwin, How Round Is Your Circle?, Princeton, NJ: Princeton University Press, 2008 pp. 188–226.

[2] A. Bogomolny. "Star Construction of Shapes of Constant Width." (Apr 16, 2013) www.cut-the-knot.org/Curriculum/Geometry/CWStar.shtml.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send