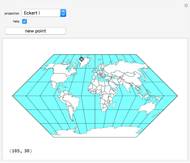
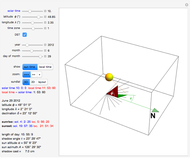
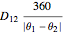Calculating the Earth's Circumference at Any Date from Any Location

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
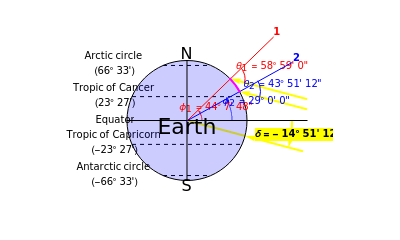
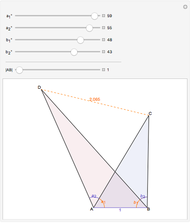
This Demonstration generalizes Eratosthenes's calculation of the Earth's circumference. The solar zenith angles 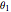 and
and 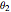 are measured at noon, on the same day, at two different locations. Knowing the distance
are measured at noon, on the same day, at two different locations. Knowing the distance 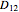 between the parallels of the two locations, the Earth's circumference is given by:
between the parallels of the two locations, the Earth's circumference is given by:
Contributed by: Philippe Brosson (October 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The latitude  is positive in the northern hemisphere and negative in the southern hemisphere. The east longitude
is positive in the northern hemisphere and negative in the southern hemisphere. The east longitude 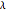 is positive and the west longitude
is positive and the west longitude 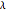 is negative.
is negative.
Examples of time zones: Paris (France): 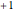 , New York:
, New York: 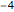 .
.
Latitudes are limited below the Arctic circle and above the Antarctic circle: 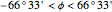 .
.
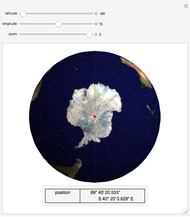
Snapshot 1: The date is February 10, 2011.
Location 1 is Lafrançaise (France), latitude 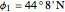 , longitude
, longitude 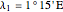 , noon is at 13:9:16 local time,
, noon is at 13:9:16 local time, 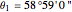 .
.
Location 2 is Meerut (India), latitude 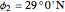 , longitude
, longitude 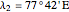 , noon is at 12:33:28 local time,
, noon is at 12:33:28 local time, 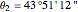 .
.
 . The distance
. The distance 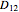 between the parallel of Lafrançaise and the parallel of Meerut is
between the parallel of Lafrançaise and the parallel of Meerut is 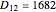 km, which gives 40030 km for the Earth's circumference. Reported measurements are
km, which gives 40030 km for the Earth's circumference. Reported measurements are 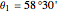 ,
, 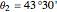 [1].
[1].
You can find details on Lafrançaise (France) at [2] and on Meerut (India) at [3].
Snapshot 2: This case reproduces Eratosthenes's original measurement of the Earth's circumference in Alexandria and Aswan on summer solstice. The date is June 21, 2012 (summer solstice).
Location 1 is Alexandria (Egypt), latitude 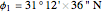 , longitude
, longitude 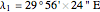 ,
, 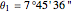 .
.
Location 2 is Aswan (Egypt), latitude 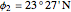 , longitude
, longitude 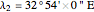 ,
, 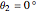 .
.
Actually, the latitude at Aswan is 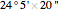 , but we use the latitude of the Tropic of Cancer (
, but we use the latitude of the Tropic of Cancer (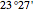 ) to agree with Eratosthenes's knowledge that at Aswan, on the summer solstice (June 21) at noon, the sun shines straight down a well.
) to agree with Eratosthenes's knowledge that at Aswan, on the summer solstice (June 21) at noon, the sun shines straight down a well.
The distance 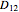 between the parallel of Alexandria and the parallel of Aswan is
between the parallel of Alexandria and the parallel of Aswan is  km, which gives 40030 km for the Earth's circumference. Eratosthenes assumed that Alexandria and Aswan belong to the same meridian; the small difference in longitude explains the slightly different local noon times.
km, which gives 40030 km for the Earth's circumference. Eratosthenes assumed that Alexandria and Aswan belong to the same meridian; the small difference in longitude explains the slightly different local noon times.
Eratosthenes found 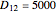 stadia and measured
stadia and measured 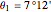 , which leads to the Earth's circumference being 39250 km, assuming a stadium value of 157 m [4].
, which leads to the Earth's circumference being 39250 km, assuming a stadium value of 157 m [4].
Snapshot 3: The date is August 13, 2012.
Location 1 is Paris (France), latitude 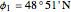 , longitude
, longitude 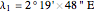 , noon at 13:55:31 local time,
, noon at 13:55:31 local time, 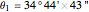 .
.
Location 2 is Rio de Janeiro (Brazil), latitude 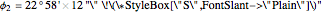 , longitude
, longitude 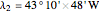 , noon at 11:57:343 local time,
, noon at 11:57:343 local time, 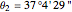 .
.
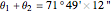 . The distance
. The distance 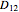 between the parallel of Paris and the parallel of Rio de Janeiro is
between the parallel of Paris and the parallel of Rio de Janeiro is 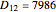 km, which gives 40030 km for the Earth's circumference.
km, which gives 40030 km for the Earth's circumference.
Snapshot 4: If Eratosthenes had lived in Brazil, he could have measured the circumference of the Earth in São Paulo (almost on the tropic of Capricorn) and Porto Alegre on the summer solstice (December 21 in the southern hemisphere) and obtained the same result.
References
[1] "Eratosthenes." (Oct 4, 2012) www.eratosthenes.eu/spip.
[2] "Eratosthenes 2010–2011." (Oct 4, 2012) eratosthenes2010.free.fr/spip.php?article78.
[3] "Eratosthenes 2010–2011." (Oct 4, 2012)eratosthenes2010.free.fr/spip.php?article79.
[4] Wikipedia. "Eratosthenes." (Oct 4, 2012) en.wikipedia.org/wiki/Eratosthenes.
[5] W. B. Stine, M. Geyer, and S. R. Stine, Power from the Sun, Chap. 3, "The Sun's Position," 2010. www.powerfromthesun.net/Book/chapter03/chapter03.html#Equation%20of%20Time.
[6] Time and Date. "The World Clock." (Oct 4, 2012) www.timeanddate.com/worldclock.
[7] The GPS Coordinates Search Engine. (Oct 4, 2012) www.thegpscoordinates.com.
Permanent Citation