Chaotic Dynamics of a Modulated Semiconductor Laser


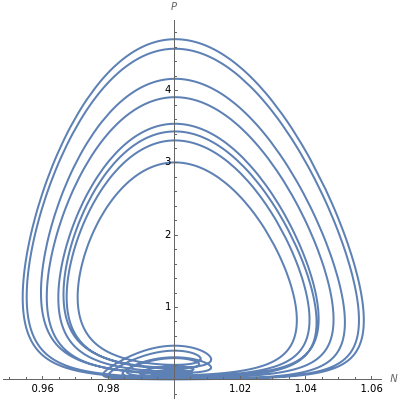
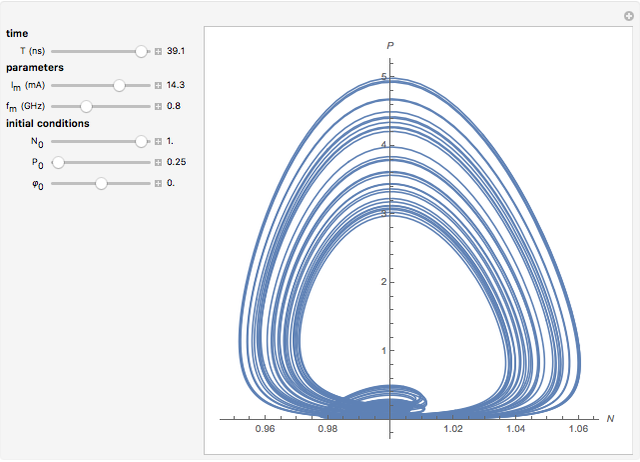
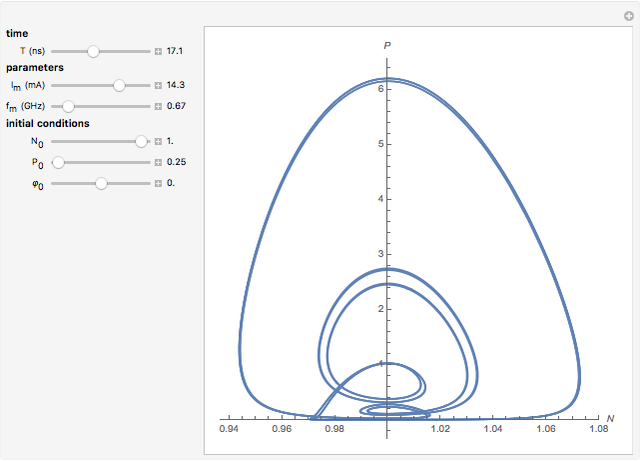
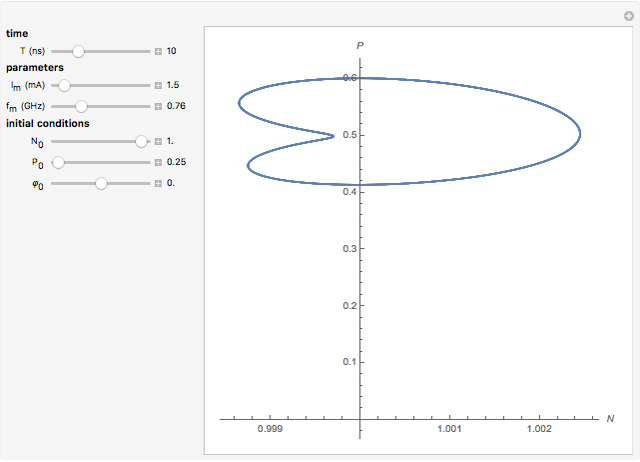
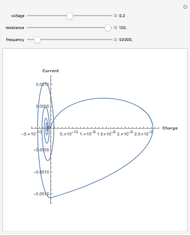
	This Demonstration shows the phase space of a modulated semiconductor laser. The parameters are 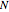, the normalized carrier density; 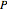, the normalized photon density; 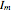(mA), the amplitude of the modulation current; and 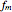(GHz), the frequency of modulation. The system exhibits both chaotic and periodic oscillations as you vary the amplitude and frequency of modulation.


	Contributed by: Manu P. John and V. M. Nandakumaran

Chaotic behavior in semiconductor lasers is well understood [1]. The peak output power of such lasers varies chaotically. The importance of chaotic behavior in semiconductor lasers is due to its potential use in the field of chaotic encryption based cryptography [2]. The dynamical equations of a modulated semiconductor laser can be written as follows:

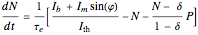
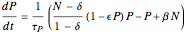
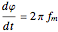The standard parameter values for chaos:

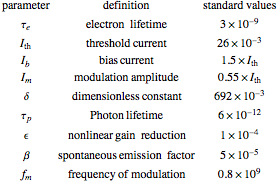
References:

[1] G. P. Agrawal, "Effect of Gain Nonlinearities on Period Doubling and Chaos in Directly Modulated Semiconductor Lasers," Applied Physics Letters, 49(16), 1986 pp. 1013–1015.

[2] V. Bindu and V. M. Nandakumaran, "Chaotic Encryption Using Long-Wavelength Directly Modulated Semiconductor Lasers," Journal of Optics A: Pure and Applied Optics, 4(2), 2002 pp. 115–119.