Complex Networks from Simple Rewrite Rules

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
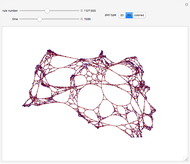
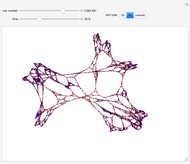
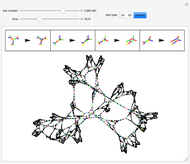
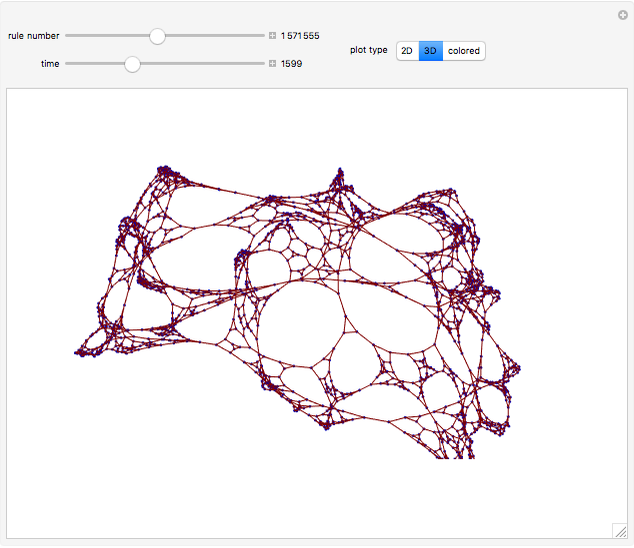
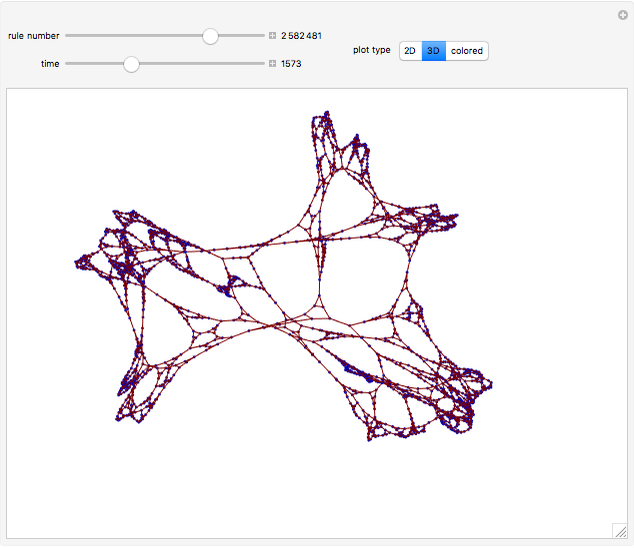
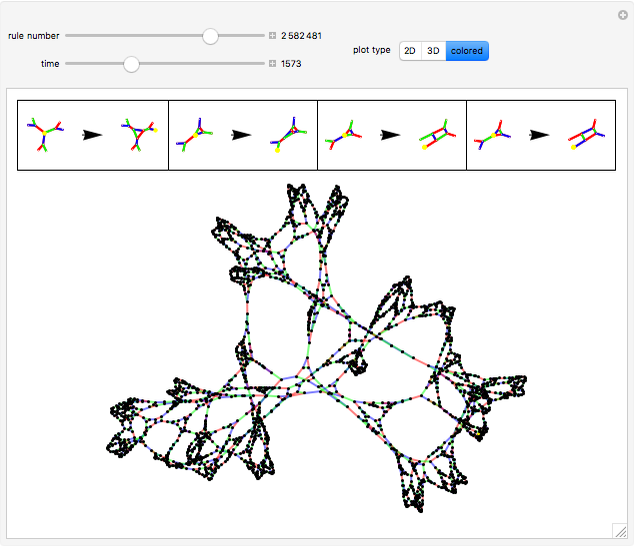
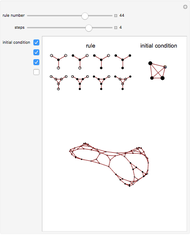
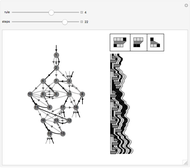
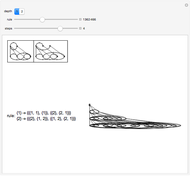
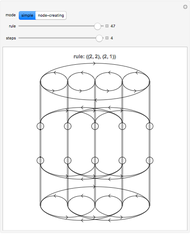
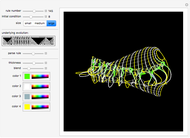
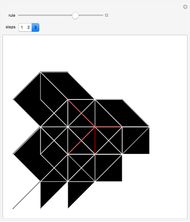
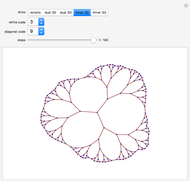
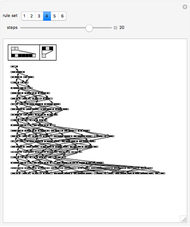
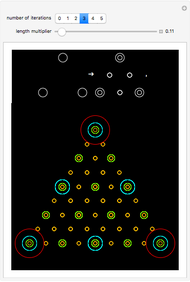
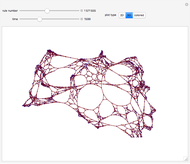
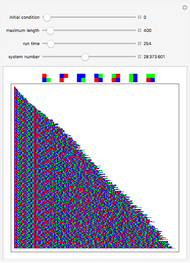
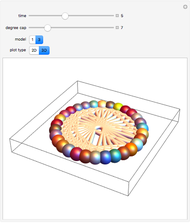
These simple rewrite systems can produce a wide variety of complex networks reminiscent of natural forms. Each time step a local rewrite operation is applied about the writer (yellow node), and then the writer moves in a way dependent upon its surroundings. Evolution begins from the cube, and uses the structural replacement rules shown. Edges are colored red, blue, and green in order to orient the writer's movement (e.g., we could have the writer move along a blue edge, and then a green edge, after encountering some particular surrounding).
Contributed by: Richard Southwell (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
By exploring the dynamics of these systems one finds an exotic variety of different forms that can be produced by very similar rules. This is similar to the case in biology, where a small change in the genetic program can profoundly effect the growth process. Classifying the different network growth processes in our systems is a fascinating task which we have only just begun [1]. So far we have found systems that generate large networks and then halt, systems that produce serially repeating parts (like plant stems), systems that produce fractal networks, and systems that produce more complex networks. It is remarkable that the simple rules behind these systems (which just involve looking at the colors of the edges linking the writer's neighbors, doing a structural modification, and moving the writer up to two hops) can produce such rich behavior. These systems have some similarities to the mobile automata and cellular automata considered in [2], the planar network rewrite systems considered in [3], and the intricate self-replicating networks considered in [4]. In [2], Wolfram suggests that the universe could be modeled as a network growing via simple rules. If this is true, then understanding the types of behavior which simple network rewrite systems can produce should be of great importance.
References
[1] R. Southwell, J. Huang, and C. Cannings, "Complex Networks from Simple Rules," Complex Systems 22(2), 2013, pp. 151–173. www.complex-systems.com/pdf/22-2-2.pdf.
[2] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media, Inc., 2002.
[3] T. Bolognesi, "A Pseudo-Random Network Mobile Automaton with Linear Growth," Information Processing Letters, 109(13), 2009, pp. 668–674. doi:10.1016/j.ipl.2009.02.023.
[4] R. Southwell and C. Cannings, "Some Models of Reproducing Graphs: III Game Based Reproduction," Applied Mathematics 1(5), 2010 pp. 335–343. doi:10.4236/am.2010.15044.
[5] R. Southwell. Complex Networks, Simple Rules. [Video]. (Dec 12, 2013) www.youtube.com/watch?v=bzvO92Gta9E.
[6] R. Southwell. How to Create Beautiful Complex Shapes Easily. [Video]. (Dec 12, 2013) www.youtube.com/watch?v=VQiGK5pLz5c.
[7] R. Southwell. How to Design and 3D Print a Complex Network. [Video]. (Dec 12, 2013) www.youtube.com/watch?v=coQnOAa9FTc.
Permanent Citation
"Complex Networks from Simple Rewrite Rules"
http://demonstrations.wolfram.com/ComplexNetworksFromSimpleRewriteRules/
Wolfram Demonstrations Project
Published: December 16 2013