Coupler Curves of a Four-Bar Linkage

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
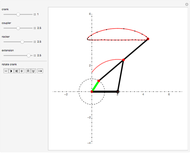
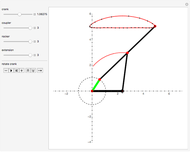
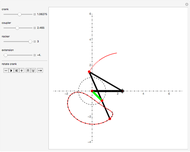
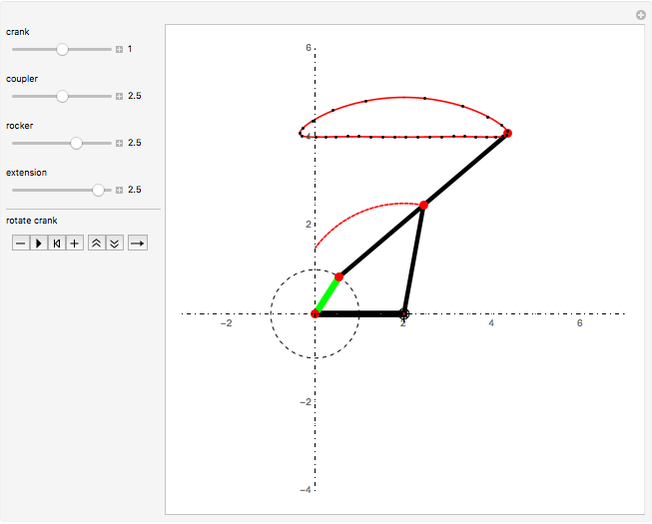
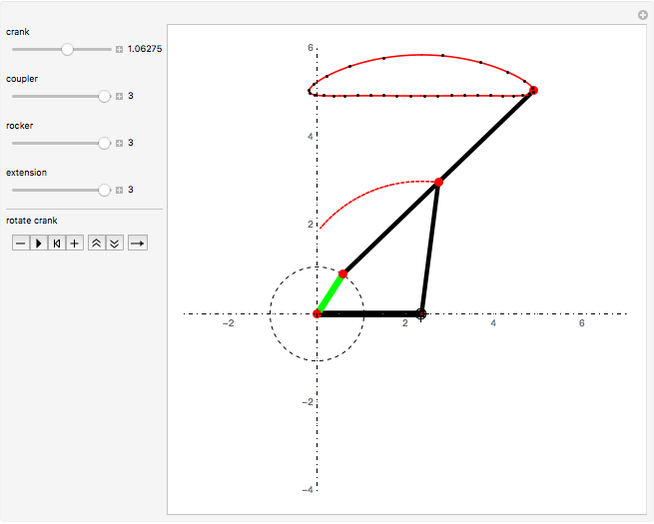
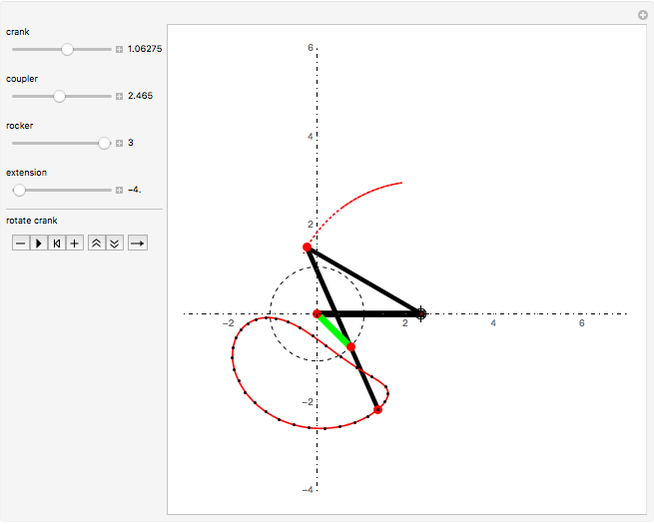
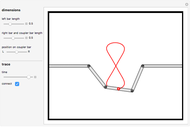
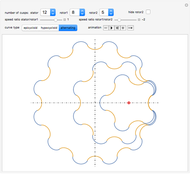
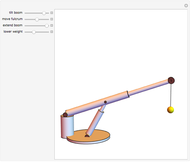
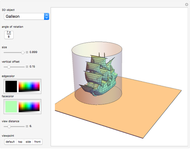
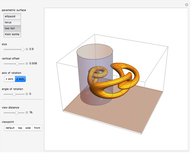
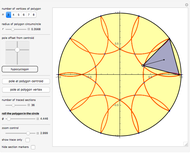
This Demonstration simulates a planar four-bar linkage mechanism and computes the path traced by a point on its coupler bar.
[more]
Contributed by: Erik Mahieu (November 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Grashof's law [1] states that the sum of the longest and the shortest link must be less than or equal to the sum of the remaining two links. This condition must be met to allow at least one link to make a complete revolution.
The four-bar linkage of this Demonstration has four joints (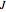 ) and a total of four links (
) and a total of four links (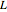 ), of which one is grounded (
), of which one is grounded (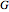 ). According to Gruebler's equation for planar mechanisms [2], the number of degrees of freedom is
). According to Gruebler's equation for planar mechanisms [2], the number of degrees of freedom is 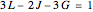 .
.
The Freudenstein equation [3] is used to compute the kinematics of a four-bar linkage.
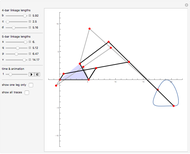
The Hoekens linkage [4] generates an almost rectilinear coupler curve. The Chebyshev lambda mechanism is very similar. See the bookmarks, snapshots 1 and 2, and the Demonstration "Chebishevs Lambda Mechanism" by Nikita Panyunin.
References
[1] "Grashof's Law." eNotes: Mechanical Engineering. engineeronadisk.com/notes_mechanic/mechanismsa6.html.
[2] A. Tchako. "Degree of Freedom." Union College Mechanical Engineering (MER 312: Dynamics and Kinematics (of Mechanisms)). (2008) www.engineering.union.edu/~tchakoa/mer312/Lectures/Lecture%202.pdf.
[3] A. Ghosal, "The Freudenstein Equation: Design of Four-Link Mechanisms," Resonance, 15(8), 2010 pp. 699–710.
[4] Wikipedia. "Hoekens Linkage." (Sept 7, 2012) en.wikipedia.org/wiki/Hoekens_linkage.
Permanent Citation
"Coupler Curves of a Four-Bar Linkage"
http://demonstrations.wolfram.com/CouplerCurvesOfAFourBarLinkage/
Wolfram Demonstrations Project
Published: November 5 2012