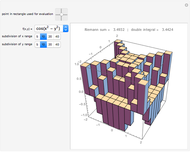
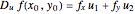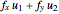Directional Derivatives and the Gradient

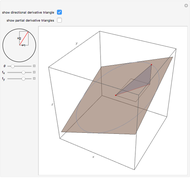
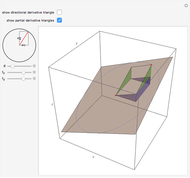
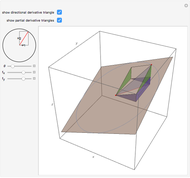
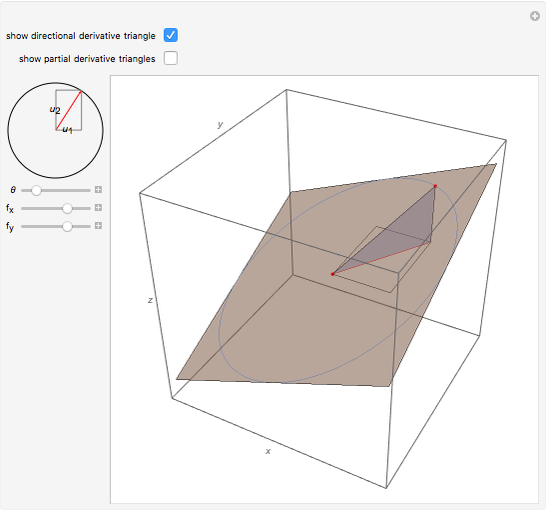
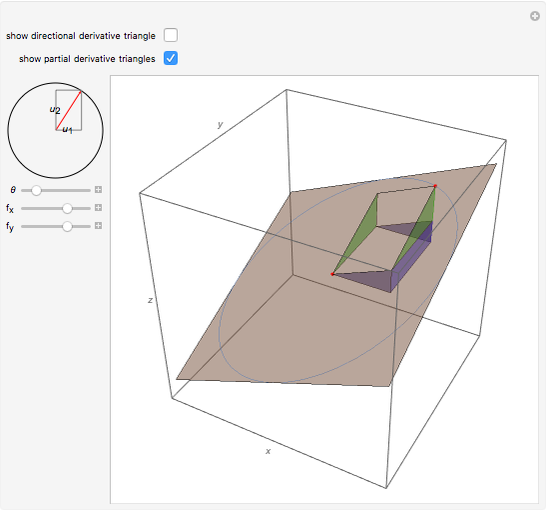
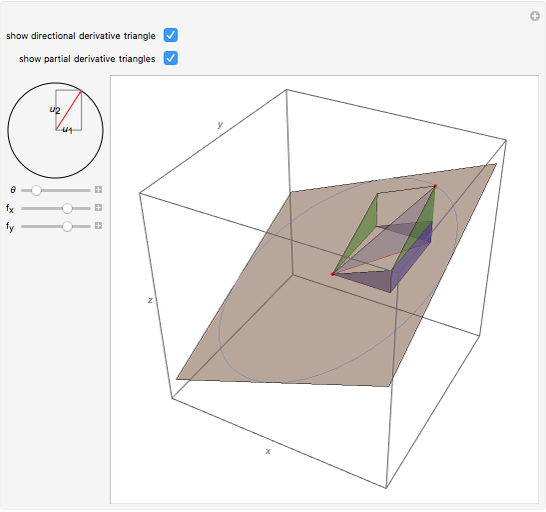
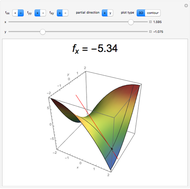
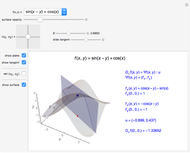
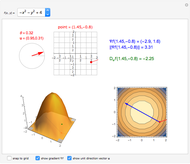
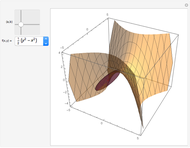
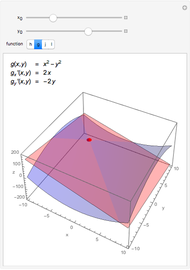
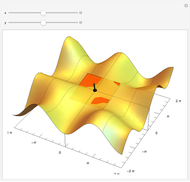
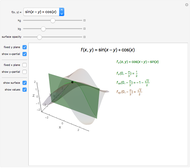
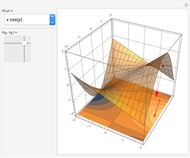
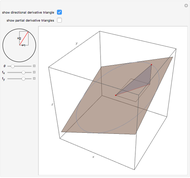
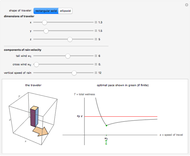
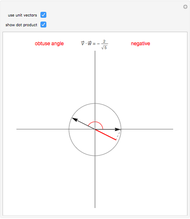
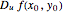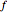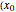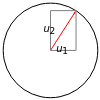
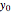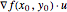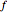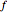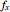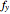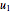This Demonstration visually explains the theorem stating that the directional derivative of the function at the point , ) in the direction of the unit vector is equal to the dot product of the gradient of with . If we denote the partial derivatives of at this point by and and the components of the unit vector by and 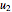, we can state the theorem as follows:

.

In this Demonstration there are controls for , the angle that determines the direction vector , and for the values of the partial derivatives and . The partial derivative values determine the tilt of the tangent plane to at the point , ); this is the plane shown in the graphic. When you view the "directional derivative triangle", observe that its horizontal leg has length 1 (since is a unit vector), and so the signed length of its vertical leg repesents the value of the directional derivative . When you view the "partial derivative triangles", this signed vertical distance is decomposed as the sum . The first summand is represented by the vertical leg of the blue triangle; the second is represented by the vertical leg of the green triangle. The visual representation is most clear when the two summands have the same sign.