Egg-Shaped Orbits of Non-Uniform Oscillators

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
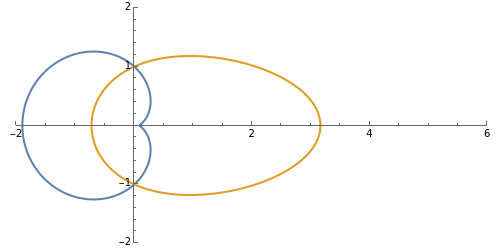
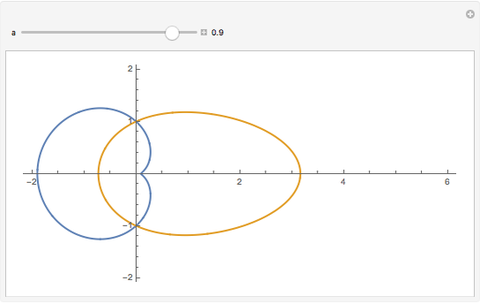
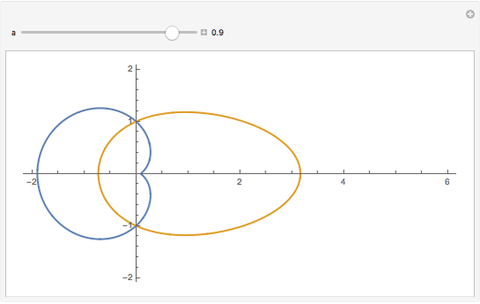
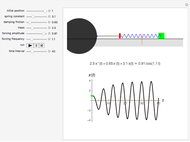
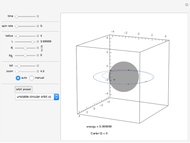
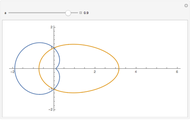
A simple non-uniform oscillator follows the differential equation 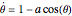 (the blue curve). In an imaginary solar system where the planets follow this law of motion, but where angular momentum is conserved, planetary orbits would be egg-shaped (the red curve), with the parameter
(the blue curve). In an imaginary solar system where the planets follow this law of motion, but where angular momentum is conserved, planetary orbits would be egg-shaped (the red curve), with the parameter  taking a role akin to the orbit eccentricity.
taking a role akin to the orbit eccentricity.
Contributed by: Andrew Read (January 2009)
After work by: Steven H. Strogatz
Open content licensed under CC BY-NC-SA
Snapshots
Details
We are able to plot both the angular velocity (blue curve) and distance from the origin (red curve) on the same axes for comparison by casting the equations in dimensionless form. For visual convenience we also define the functions so that when the oscillation is uniform, both the angular velocity and distance from the origin are equal to unity, as described below:
The curves are related by the need to keep the angular momentum equal to a constant, 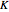 . As an equation we therefore have,
. As an equation we therefore have, 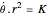 . We define the angular velocity with
. We define the angular velocity with 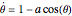 (you can vary
(you can vary  with the slider control), then define
with the slider control), then define  , and obtain
, and obtain 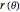 as a result.
as a result.
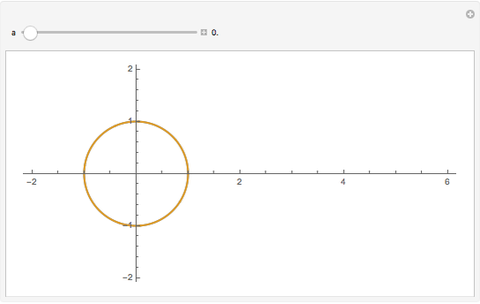
In the case where the non-uniformity  is zero, we have constant angular velocity with an intuitively expected circular orbit. When the non-uniformity
is zero, we have constant angular velocity with an intuitively expected circular orbit. When the non-uniformity  becomes significant at around 0.9, the angular velocity becomes very small in the region near
becomes significant at around 0.9, the angular velocity becomes very small in the region near 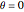 . To compensate, the orbital radius grows very large, hence an egg-shaped orbit. As
. To compensate, the orbital radius grows very large, hence an egg-shaped orbit. As  approaches unity, the orbital radius must approach infinity and the orbit is then no longer closed.
approaches unity, the orbital radius must approach infinity and the orbit is then no longer closed.
Permanent Citation