European Option Prices and Greeks in 3D

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
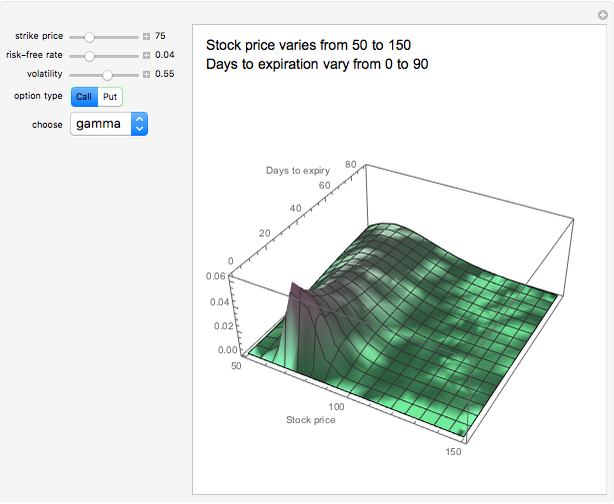
This Demonstration displays the prices of European call options, put options, or the "Greeks" associated with these options (delta, gamma, vega, theta, and rho). The display is 3D, with the stock price on the  axis and the days to expiration on the
axis and the days to expiration on the  axis. Sliders let you change the strike price, risk-free rate, and volatility parameters. You can see how a specific parameter realization travels across the 3D surface as the stock price changes and time to expiration approaches.
axis. Sliders let you change the strike price, risk-free rate, and volatility parameters. You can see how a specific parameter realization travels across the 3D surface as the stock price changes and time to expiration approaches.
Contributed by: Joseph D. Haley (November 2012)
(St. Cloud State University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: Rotate the view slightly to look under the surface. It shows the delta curve at 90 days to expiration as a smooth, cumulative normal distribution. As time to expiration approaches, this curve becomes very steep, showing the increased difficulty of maintaining an accurate delta hedge.
Snapshot 2: The gamma parameter spikes when the option is near expiration and the stock price is near the strike price. This (relatively) large value corresponds with the steepness of the delta curve under the same circumstances.
Snapshot 3: Rotate the view to a two-dimensional display showing that the vega parameter shrinks as expiration approaches. The horizontal grid lines represent a fixed stock price.
Permanent Citation
"European Option Prices and Greeks in 3D"
http://demonstrations.wolfram.com/EuropeanOptionPricesAndGreeksIn3D/
Wolfram Demonstrations Project
Published: November 29 2012