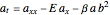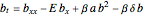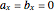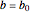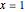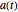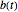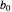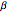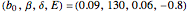Gray-Scott Reaction-Diffusion Cell with an Applied Electric Field

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
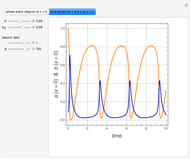
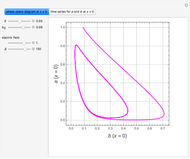
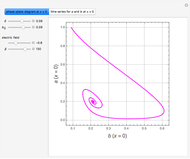
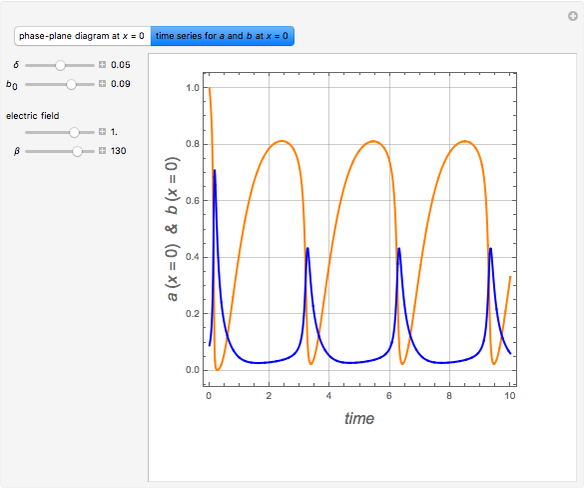
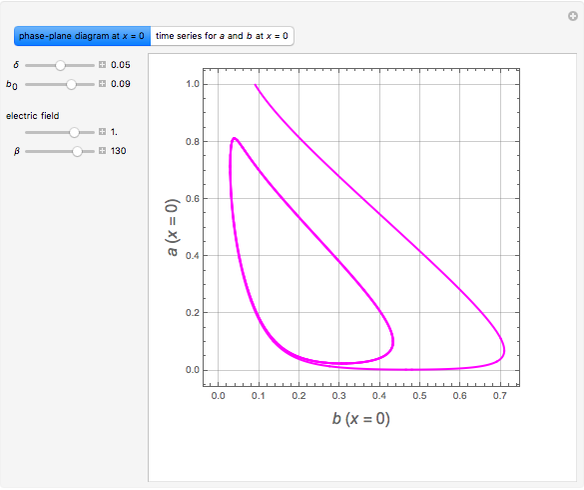
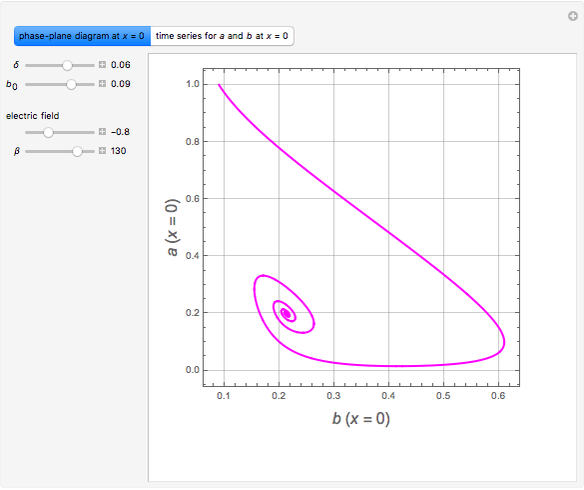
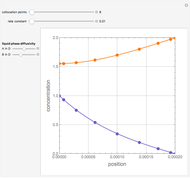
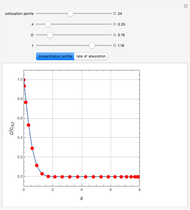
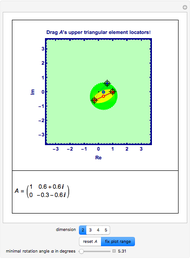
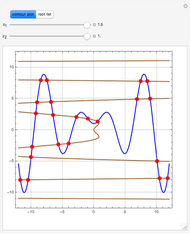
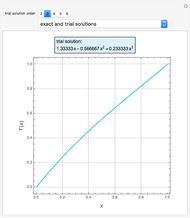
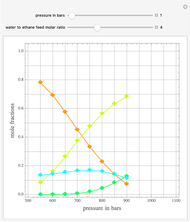
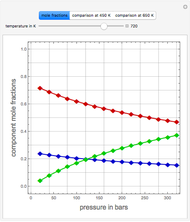
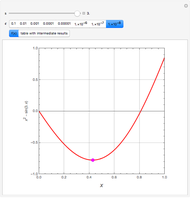
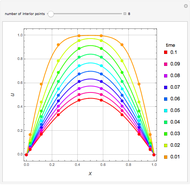
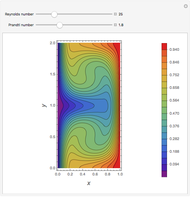
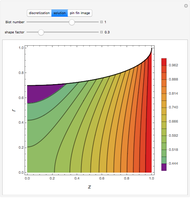
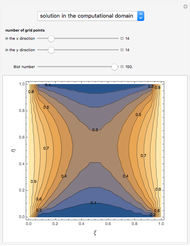
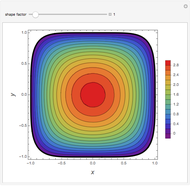
Consider the Gray–Scott reaction-diffusion cell with an applied electric field. The governing equations and boundary and initial conditions are:
[more]
Contributed by: Housam Binousand Brian G. Higgins (June 2013)
Open content licensed under CC BY-NC-SA
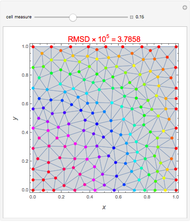
Snapshots
Details
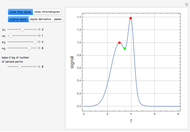
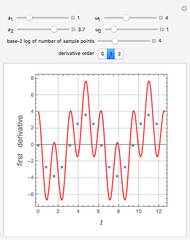
In the discrete Chebyshev–Gauss–Lobatto case, the interior points are given by 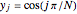 . These points are the extrema of the Chebyshev polynomials of the first kind,
. These points are the extrema of the Chebyshev polynomials of the first kind, 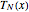 .
.
The 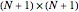 Chebyshev derivative matrix at the quadrature points is an
Chebyshev derivative matrix at the quadrature points is an 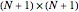 matrix
matrix 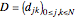 given by
given by
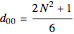 ,
, 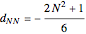 ,
, 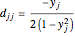 for
for 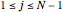 , and
, and 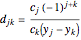 for
for 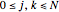 and
and 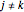 ,
,
where 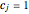 for
for 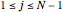 and
and 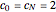 .
.
The matrix 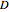 is then used as follows:
is then used as follows: 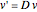 and
and 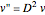 , where
, where  is a vector formed by evaluating
is a vector formed by evaluating  at
at 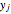 ,
, 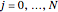 , and
, and 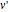 and
and 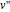 are the approximations of
are the approximations of 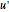 and
and 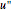 at the
at the 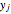 .
.
Reference
[1] P. Moin, Fundamentals of Engineering Numerical Analysis, Cambridge, UK: Cambridge University Press, 2001.
[2] L. N. Trefethen, Spectral Methods in Matlab, Philadelphia: SIAM, 2000.
[3] A. W. Thornton and T. R. Marchant, "Semi-analytical solutions for a Gray–Scott reaction–diffusion cell with an applied electric field," Chemical Engineering Science, 63(2), 2008 pp. 495–502. DOI: 10.1016/j.ces.2007.10.001 .
Permanent Citation