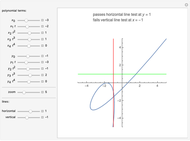
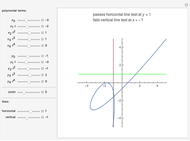
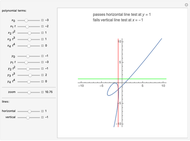
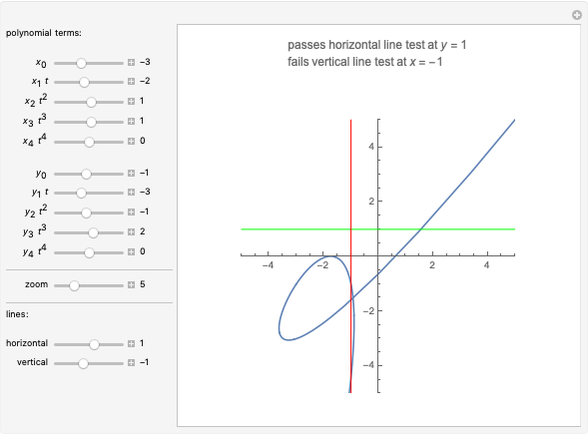
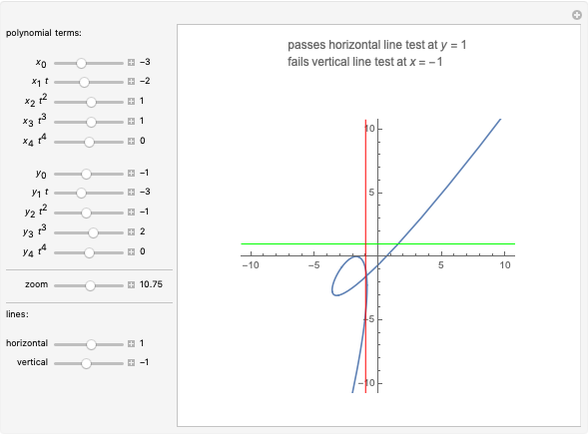
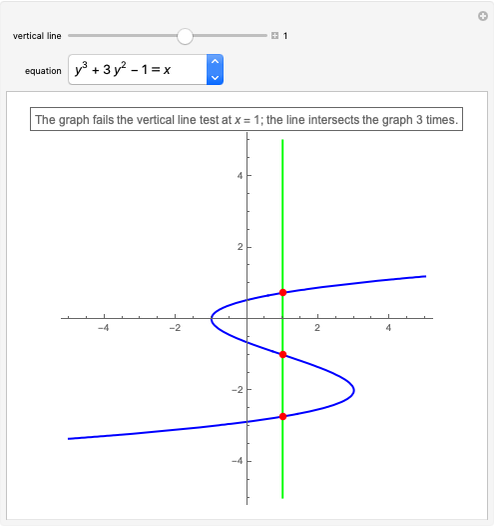
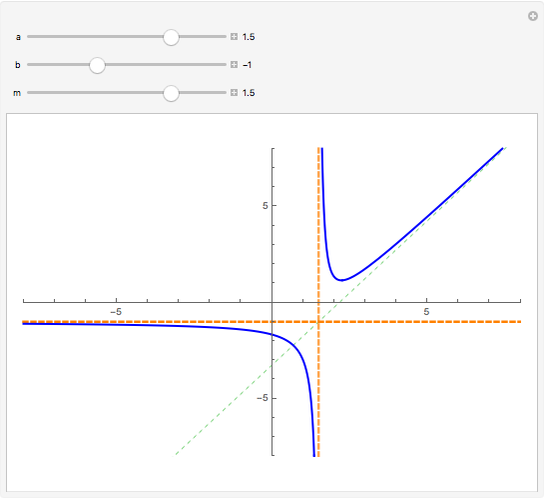
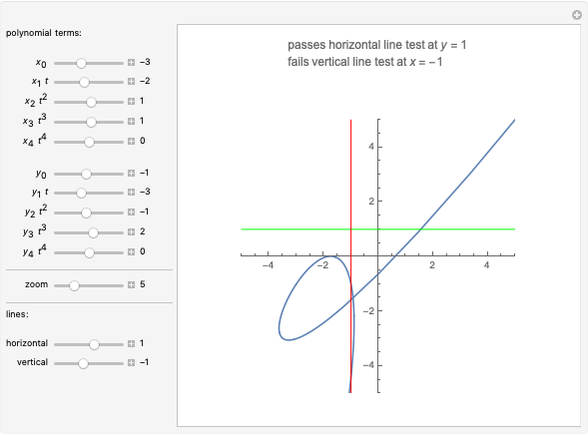
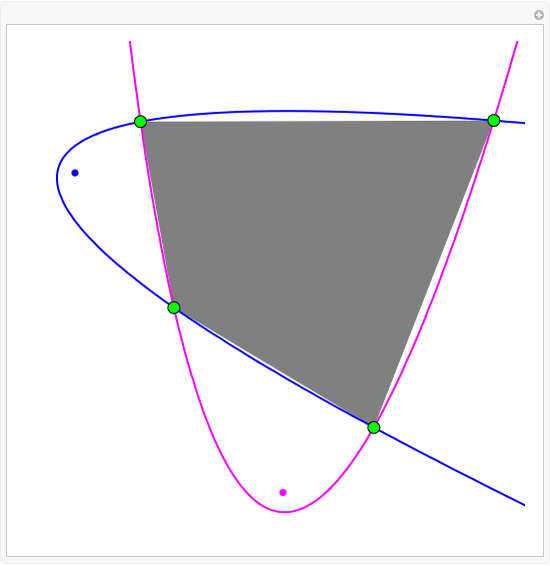
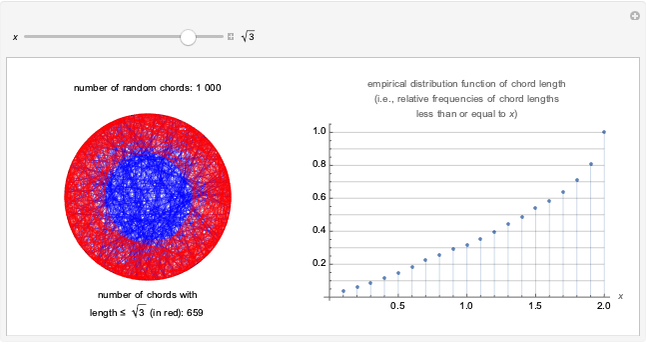
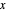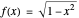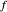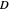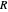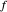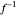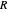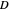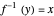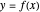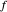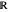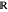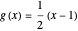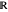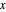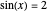When every element in the domain corresponds to exactly one element in the range, the relation is a function. A function passes the vertical line test: no vertical line passes through more than one point in the relation. The unit circle is thus not a function. The half-circle above the 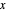 axis is the function
axis is the function 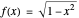 .
.
The horizontal line test, which tests if any horizontal line intersects a graph at more than one point, can have three different results when applied to functions:
1. If no horizontal line intersects the function in more than one point, the function is one-to-one (or injective).
2. If every horizontal line intersects the function in at least one point, it is onto (or surjective).
3. If every horizontal line intersects the function in exactly one point, it is one-to-one and onto (or bijective).
Suppose 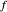 is a function with domain
is a function with domain 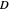 and range
and range 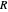 . The inverse of
. The inverse of 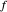 is a function
is a function 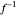 with domain
with domain 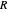 and range
and range 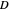 such that
such that 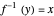 if and only if
if and only if 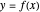 . For the inverse to exist, the original function
. For the inverse to exist, the original function 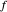 must be one-to-one and onto.
must be one-to-one and onto.
Let 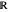 be the set of real numbers. The inverse of
be the set of real numbers. The inverse of 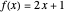 with domain and range
with domain and range 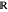 is the function
is the function 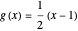 with the same domain and range.
with the same domain and range.
Many functions that come up in practice are either not one-to-one or not onto. For example, because trigonometric functions are periodic they are many-to-one on 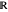 . Also, except for the tangent and arctangent functions, the trig functions are not onto. For example, there is no real number
. Also, except for the tangent and arctangent functions, the trig functions are not onto. For example, there is no real number 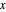 such that
such that 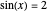 .
.
[less]

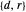 . For example, the set of points at distance 1 from the origin—whose graph is the unit circle—is a relation. The domain
. For example, the set of points at distance 1 from the origin—whose graph is the unit circle—is a relation. The domain 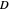 is the set of first values
is the set of first values  . The range
. The range 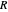 is the set of last values
is the set of last values  .
.