Limits of a Rational Function of Two Variables

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
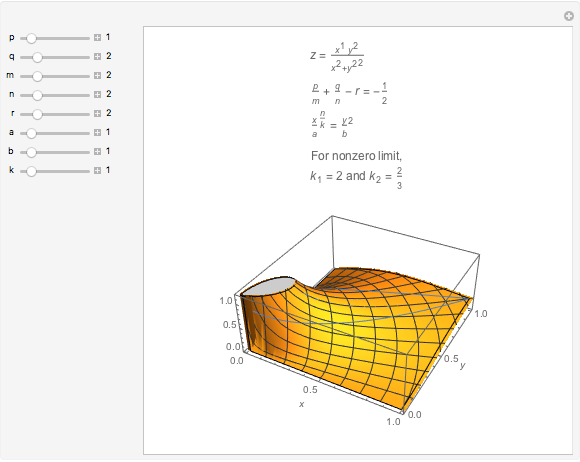
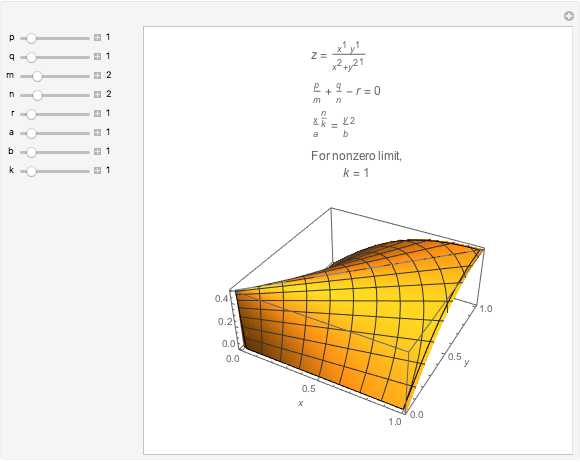
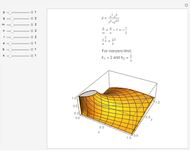
What is the behavior of 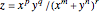 for positive
for positive  and
and 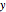 near
near  , where
, where 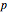 ,
,  ,
, 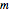 ,
,  , and
, and  are positive? This Demonstration allows you to investigate.
are positive? This Demonstration allows you to investigate.
Contributed by: Roger B. Kirchner (March 2011)
Open content licensed under CC BY-NC-SA
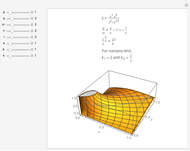
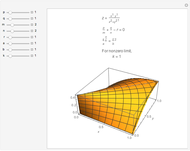
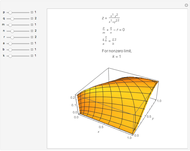
Snapshots
Details
If 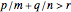 , then
, then 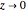 as
as 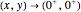 .
.
If  , then
, then  is bounded and the limit does not exist.
is bounded and the limit does not exist.
If 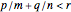 , then
, then  is unbounded.
is unbounded.
To see this, let 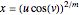 and
and 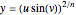 .
.
Then, 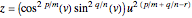 .
.
What about the limit of  along the algebraic curves
along the algebraic curves 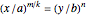 , where
, where 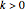 ?
?
If 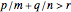 , then
, then 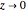 .
.
If 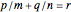 , then
, then
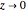 if
if 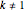 and
and
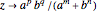 if
if 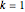 .
.
If 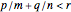 , then
, then  can have limit 0, any positive number, or ∞, depending on
can have limit 0, any positive number, or ∞, depending on  .
.
Let 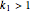 and
and 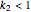 be defined by
be defined by
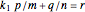 , and
, and
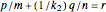 .
.
Then 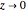 if
if 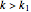 or
or 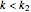 ,
,
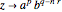 if
if 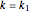 ,
,
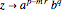 if
if 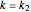 ,
,
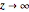 if
if 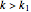 or
or 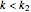 .
.
To see this, let 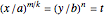 , so
, so 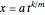 ,
, 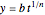 , where
, where 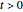 .
.
Then, 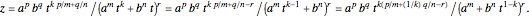
The results follow by considering the cases 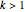 ,
, 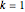 , and
, and 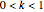 .
.
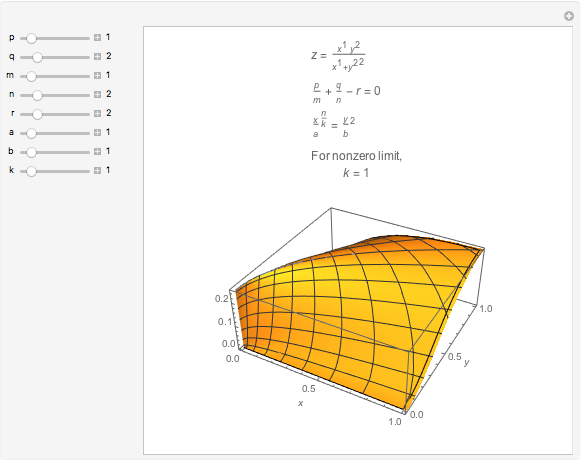
Example 1:
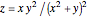
 ,
, 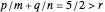
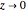 , as
, as 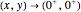 , and along any curve to the origin.
, and along any curve to the origin.
Example 2:
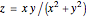
 ,
, 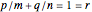
If 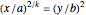 , or
, or 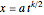 ,
, 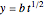 ,
,
then 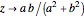 if
if 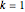 and
and 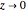 if
if 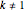 .
.
Example 3:
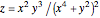
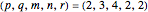 ,
, 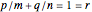
If 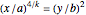 , or
, or 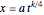 ,
, 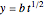 , then
, then
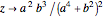 if
if 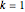 , and
, and 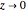 if
if 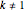 .
.
Example 4:
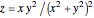
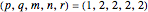 ,
, 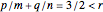
Then, 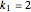 and
and 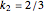 .
.
If 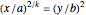 , or
, or 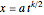 and
and 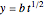 , then
, then
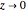 if
if 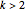 or
or 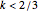 ,
,
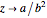 if
if 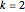 ,
,
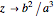 if
if 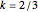 ,
,
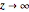 if
if 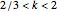 .
.
Example 5:
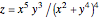
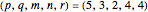 ,
, 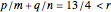
Then 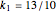 and
and 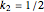
If 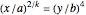 , or
, or 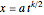 ,
, 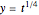 , then
, then
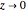 if
if 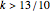 or
or 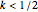 ,
,
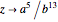 if
if 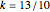 ,
,
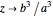 if
if 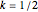 , and
, and
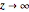 if
if 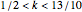 .
.
Permanent Citation