Newton's Ellipse

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
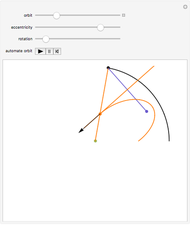
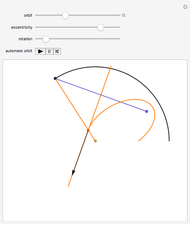
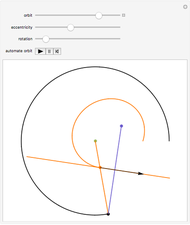
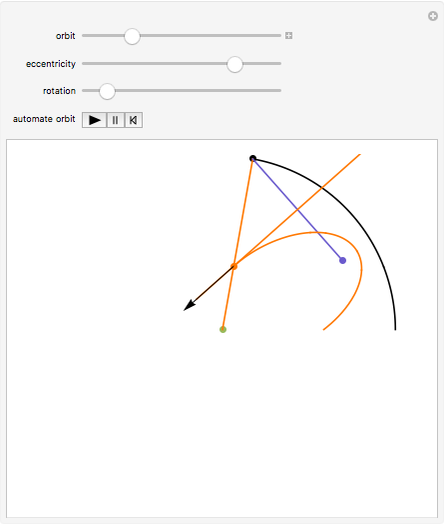
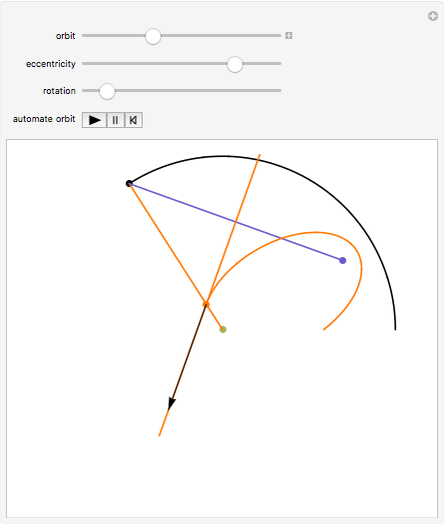
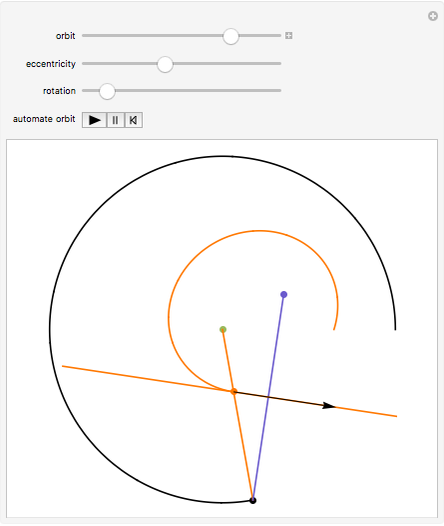
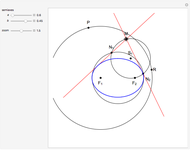
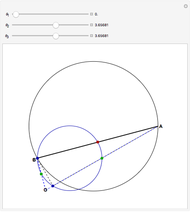
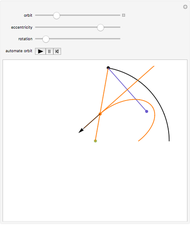
Newton showed this construction in Book 1, Section 4, Lemma 15, of Principia. On March 13, 1964, Feynman resurrected the construction and used it in a lecture, "The Motion of Planets Around the Sun". The lecture is detailed in a book with audio CD, Feynman's Lost Lecture, by David and Judith Goodstein. In the lecture, Feynman used the diagram and differential geometry to prove the planetary laws of motion.
[more]
Contributed by: Bob Rimmer (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
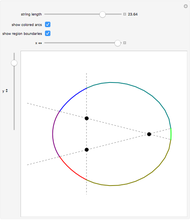
The construction is done in the complex plane, using the vector properties of complex numbers to construct the lines to the points. The equation of the circle is 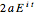 , where
, where  is the semi-major axis of the ellipse; the equation of the ellipse is
is the semi-major axis of the ellipse; the equation of the ellipse is 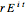 , where
, where  is the radius of the ellipse from the primary focus at that point. The construction can be redone so that the secondary focus is outside the circle, creating a hyperbola, or on the circle, where it should create a parabola. A simple geometric proof can be found in chapter 9 section 5 of Jeremy Tatum's online text Celestial Mechanics.
is the radius of the ellipse from the primary focus at that point. The construction can be redone so that the secondary focus is outside the circle, creating a hyperbola, or on the circle, where it should create a parabola. A simple geometric proof can be found in chapter 9 section 5 of Jeremy Tatum's online text Celestial Mechanics.
Permanent Citation