Predicting Maximum Sea Levels

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
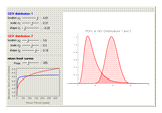
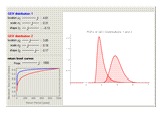
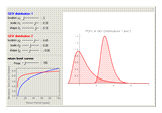
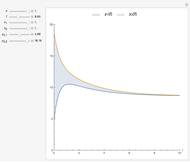
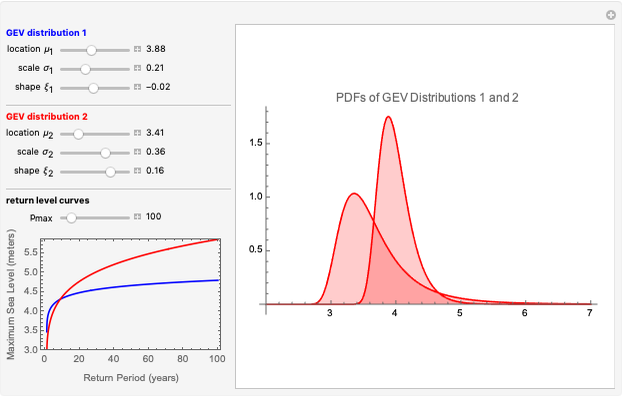
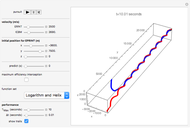
Extreme value distributions are used to model the occurrence of extrema (i.e. extreme deviations from the median of a probability distribution). The parameters for GEV Distribution 1 are taken from a model fitted to annual maximum sea level data in Port Pirie, Australia from 1923–1987. GEV Distribution 2 has the same parameters as GEV Distribution 1, only the scale parameter has been increased to create more variability. The return level curves shown in the bottom-left give the expected maximum sea level 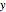 that will occur once every
that will occur once every  years. For example, the Port Pirie return curve (blue) indicates that one may expect the sea level to reach 4.3 meters once every ten years, or 4.6 meters once every 100 years.
years. For example, the Port Pirie return curve (blue) indicates that one may expect the sea level to reach 4.3 meters once every ten years, or 4.6 meters once every 100 years.
Contributed by: Scott Constable (April 2011)
With many thanks to: Tom Pfaff
Open content licensed under CC BY-NC-SA
Snapshots
Details
The generalized extreme value distribution is a combined family of three distinct distribution families: Gumbel, Fréchet, and Weibull. It is a distribution function of the form
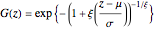 ,
,
with parameters  ,
,  , and
, and  for location, scale, and shape, respectively. Return level curves for a GEV can be generated by plotting
for location, scale, and shape, respectively. Return level curves for a GEV can be generated by plotting
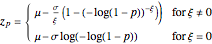
for the return period 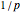 . The Port Pirie data and parameters can be found in [1]. Anyone interested in learning more about extreme value theory should also refer to [1]. Coles provides a clear and coherent overview of modeling extreme values and supplements with a variety of examples. The goal of this Demonstration was to put one of those examples into a more tangible form.
. The Port Pirie data and parameters can be found in [1]. Anyone interested in learning more about extreme value theory should also refer to [1]. Coles provides a clear and coherent overview of modeling extreme values and supplements with a variety of examples. The goal of this Demonstration was to put one of those examples into a more tangible form.
Reference
[1] S. Coles, An Introduction to Statistical Modeling of Extreme Values, London: Springer-Verlag, 2001
Permanent Citation