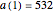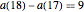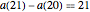Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Prime-Generating Recurrence

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

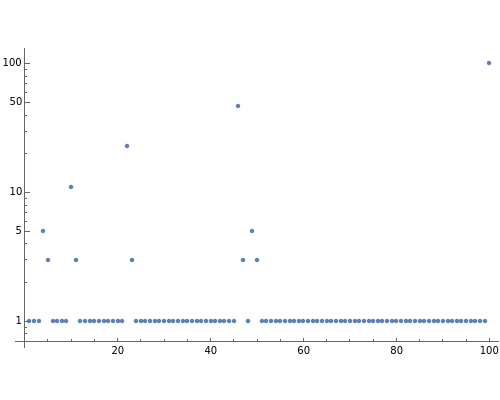
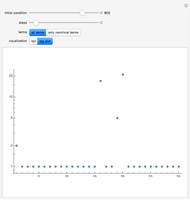
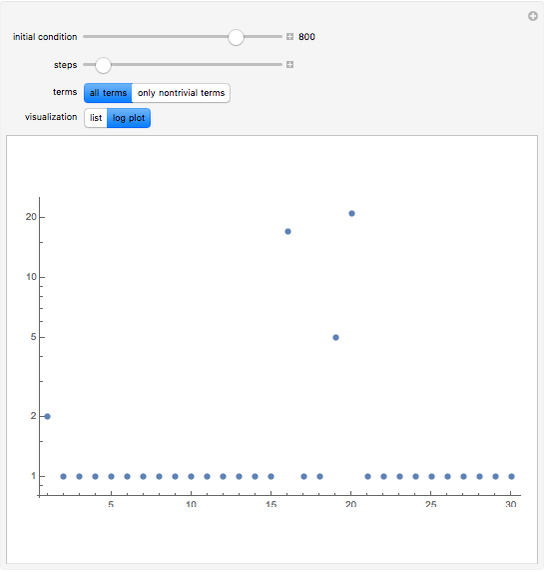
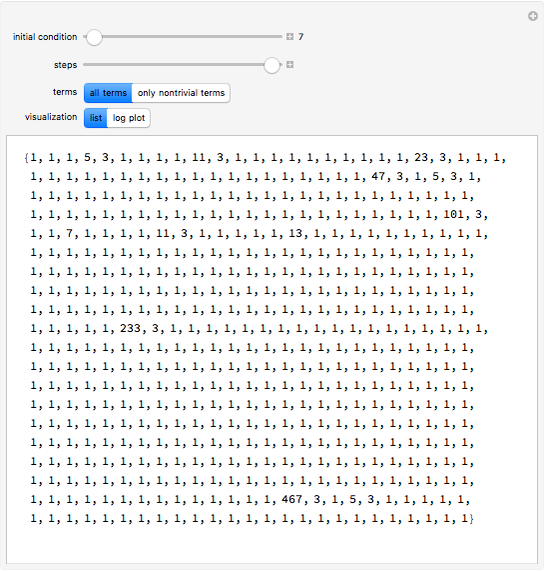
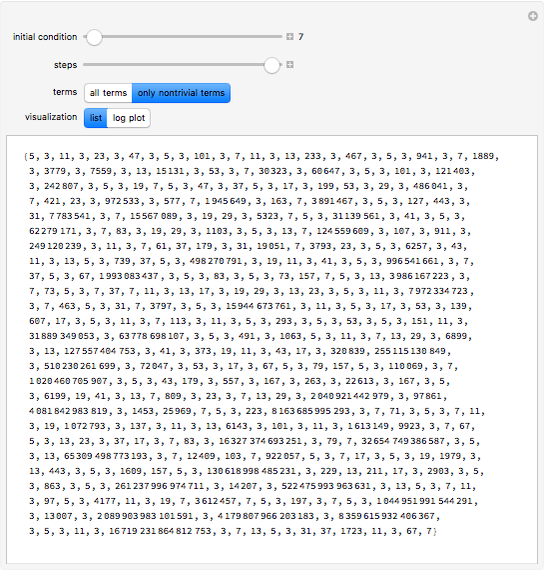
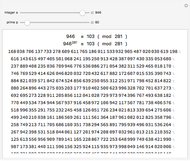
This Demonstration explores solutions of the recurrence 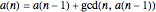through the difference sequence 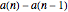, which exhibits complex behavior. For the initial condition 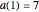, the sequence 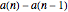consists entirely of 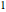s and primes, making this recurrence a rare "naturally occurring" generator of primes.

[more]

This result is not true in general: for example, letting produces , and letting produces . However, for these initial conditions, the difference sequence eventually consists entirely of s and primes. It is an unsolved problem to determine whether all initial conditions eventually produce only s and primes.

You can choose to view all terms of the difference sequence or only the terms which are not .

[less]

Contributed by: Eric Rowland (July 2008)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This recurrence was discovered at the 2003 NKS Summer School (NKS|Online) by a group led by Matt Frank.

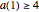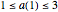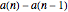This Demonstration allows initial conditions . For , is 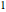for .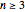

For more information, see E. S. Rowland, "A Natural Prime-Generating Recurrence," Journal of Integer Sequences [online], 11(2), 2008.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send