Random Number Generation

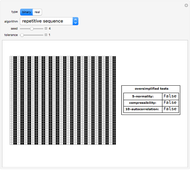
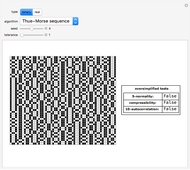
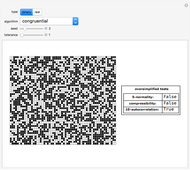
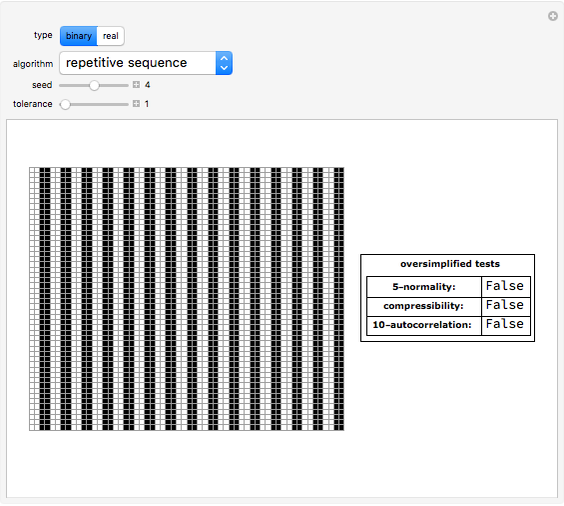
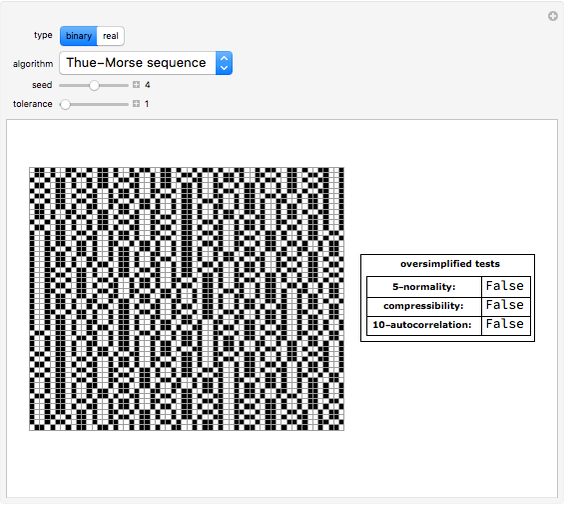
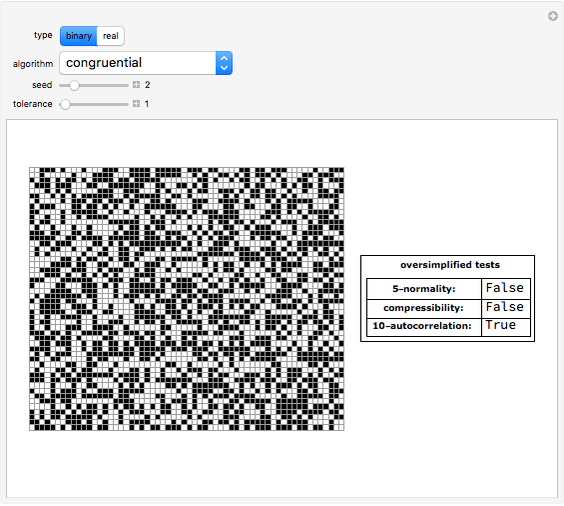
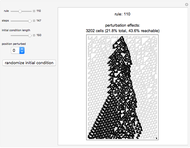
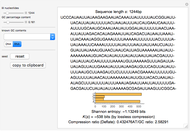
A random or pseudorandom number generator (RNG) is a computational or physical device designed to generate a random sequence of numbers. There are many different methods for generating random bits and testing their quality. This Demonstration shows all the Mathematica algorithms for producing random binary sequences and random real number sequences (between 0 and 1) with other examples (for binary sequences) that clearly fail as RNGs, such as a repetitive sequence and the Thue-Morse example.

For binary sequences, the Demonstration also includes a sample segment of random bits that was produced by a hardware device whose randomness relies on a quantum physical process and another whose randomness relies on atmospheric noise. It can be seen that all of them succeed or fail the oversimplified tests to detect the lack of randomness, either by changing the seed or by shifting the threshold of the statistical tolerance. All comparisons are made over groups of 10000 bits each (one group per seed) even when only 3000 bits are displayed.

Contributed by: Hector Zenil

Show Initialization Code

(Over 500 lines omitted)

The oversimplified tests include two common statistical tests: normality and autocorrelation. A random sequence is normal (but not the other way around). A normal sequence is a sequence whose digits show a uniform distribution, with all digits being equally likely; the 5-normality test partitions the whole sequence into substrings of length 1 to 5 and tests each for whether the standard variation of their frequency differs by an acceptable value (the statistical tolerance).

The autocorrelation test looks for possible "hidden" functions producing the sequence. It is the cross-correlation of the sequence with itself. Autocorrelation is useful for finding repeating patterns, such as periodic sequences. The oversimplified implementation of this test partitions the entire sequence into groups of 10 and then again into pairs, comparing each first segment with the second, looking for possible regularities.

The compressibility test is based on algorithmic information theory. Compression algorithms look for regularities. If the compressed version of the sequence is short enough compared to the original size of the sequence given a threshold (defined by the tolerance control), the sequence is unlikely to be random.

These tests may be useful as a first step in determining whether or not a generator obviously fails or not as an RNG. No test can prove definitively whether a nontrivial sequence (and the generator that produced it) is good enough as an RNG due to possible random or nonrandom local segments.