Complex Networks

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
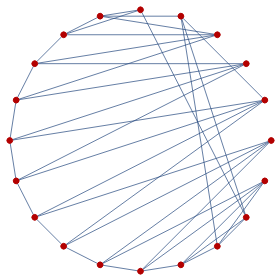
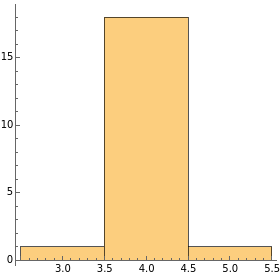
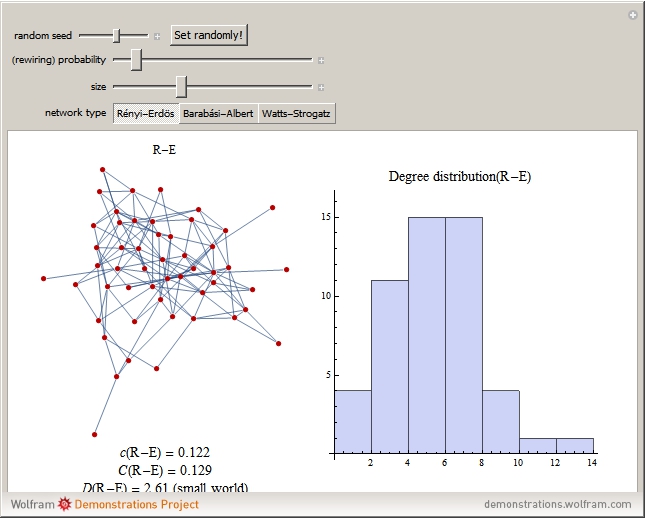
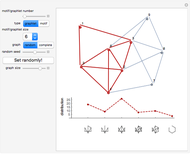
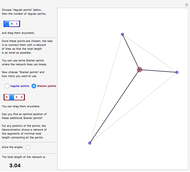
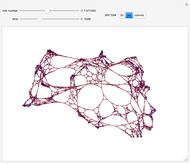
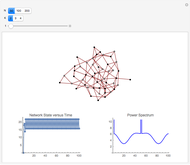
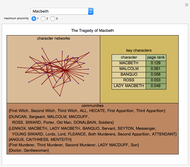
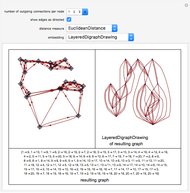
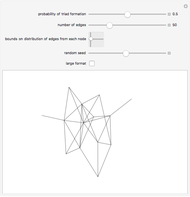
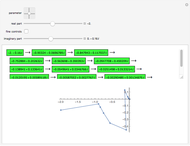
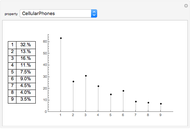
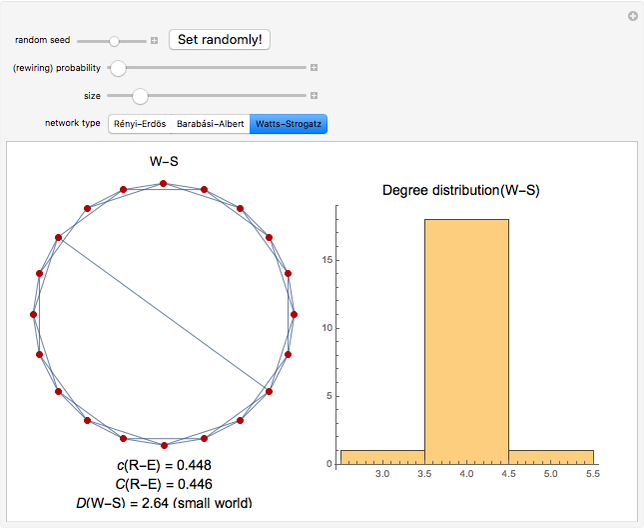
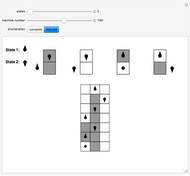
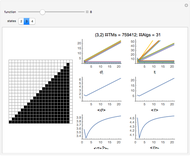
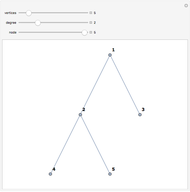
This Demonstration illustrates two models of complex networks as compared to random graphs as studied by Rényi and Erdös (R–E). The Watts–Strogattz (W–S) algorithm produces small-world networks, a property of real-world networks that keeps nodes relatively close to each other (as shown by the average distance 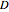 in the Demonstration). It does so by starting from a regular network (e.g. a lattice, here plotted in the traditional circular embedding). The Barabasi–Albert (B–A) algorithm of preferential attachment also produces small-world networks that are scale-free, another property common among real-world networks, such as biological networks (genetic, metabolic, etc.) and electric or social networks, to mention only a few examples. Scale-free networks produce power-law degree distributions, in contrast to the normal distribution of a random network. (The degree of a node is the number of links connected to the node). Complex networks mimic many properties of empirical networks and are robust and less expensive (in the number of links to keep the network "small") than random Rényi–Erdös networks; and of high clustering (as shown by the mean clustering coefficient
in the Demonstration). It does so by starting from a regular network (e.g. a lattice, here plotted in the traditional circular embedding). The Barabasi–Albert (B–A) algorithm of preferential attachment also produces small-world networks that are scale-free, another property common among real-world networks, such as biological networks (genetic, metabolic, etc.) and electric or social networks, to mention only a few examples. Scale-free networks produce power-law degree distributions, in contrast to the normal distribution of a random network. (The degree of a node is the number of links connected to the node). Complex networks mimic many properties of empirical networks and are robust and less expensive (in the number of links to keep the network "small") than random Rényi–Erdös networks; and of high clustering (as shown by the mean clustering coefficient  and the global clustering coefficient
and the global clustering coefficient 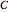 in the Demonstration) is a measure of degree to which nodes in a graph tend to cluster together.
in the Demonstration) is a measure of degree to which nodes in a graph tend to cluster together.
Contributed by: Hector Zenil (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Complex Networks"
http://demonstrations.wolfram.com/ComplexNetworks/
Wolfram Demonstrations Project
Published: October 23 2013