Rotation about a Point in the Plane

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
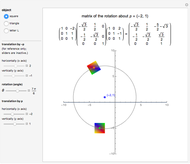
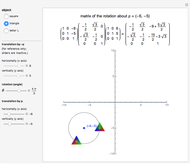
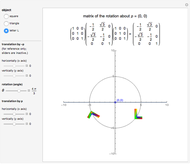
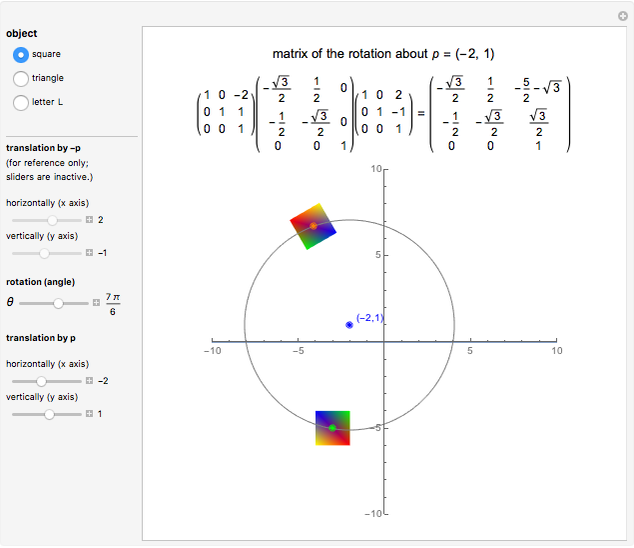
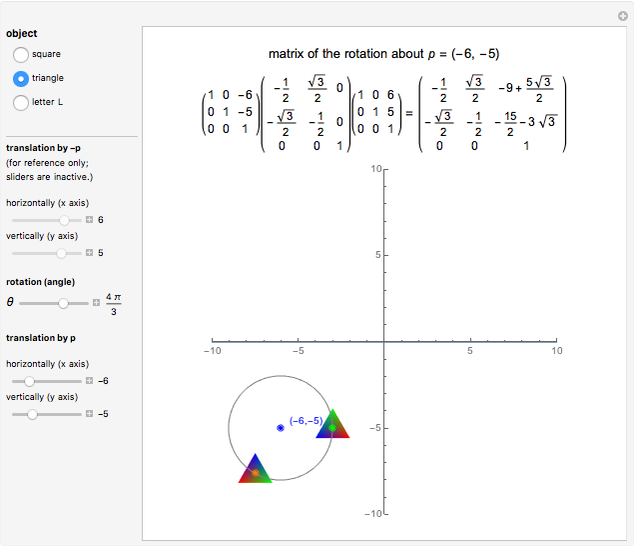
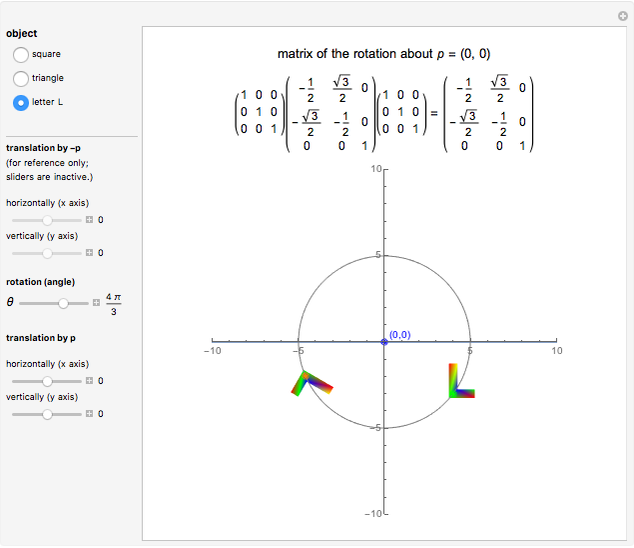
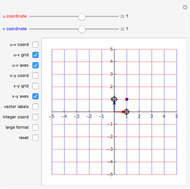
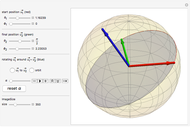
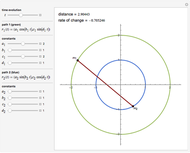
In this Demonstration you can rotate a square, a triangle, or the letter L about the point 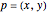 in the plane, choosing the coordinates
in the plane, choosing the coordinates 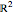 with the "translation by
with the "translation by 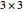 " sliders or by dragging the point in the graphic. Change the angle
" sliders or by dragging the point in the graphic. Change the angle 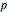 to see the rotation about the point
to see the rotation about the point 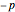 . The
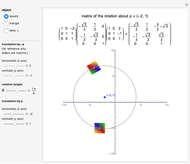
. The 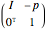 matrix of the rotation is given by the product of three operations (from right to left): translation by
matrix of the rotation is given by the product of three operations (from right to left): translation by  , rotation around the origin, and translation back by
, rotation around the origin, and translation back by 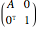 .
.
Contributed by: Ana Moura Santos, Pedro A. Santos, and João Pedro Pargana (January 2011)
(Instituto Superior Técnico)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation
"Rotation about a Point in the Plane"
http://demonstrations.wolfram.com/RotationAboutAPointInThePlane/
Wolfram Demonstrations Project
Published: January 5 2011