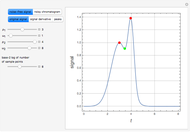
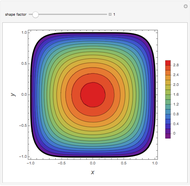
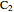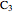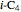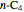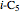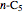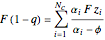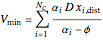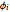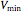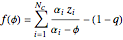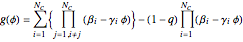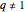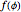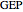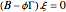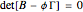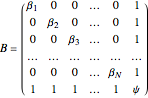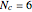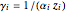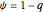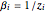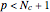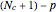Solution of the First Underwood Equation Formulated as a Generalized Eigenvalue Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
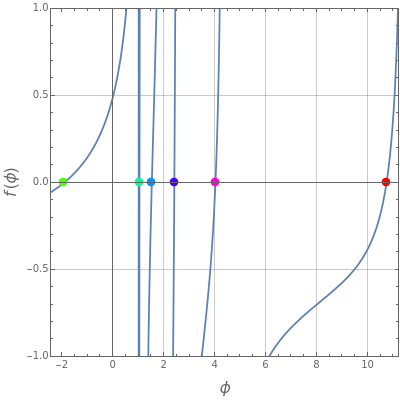
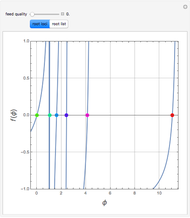
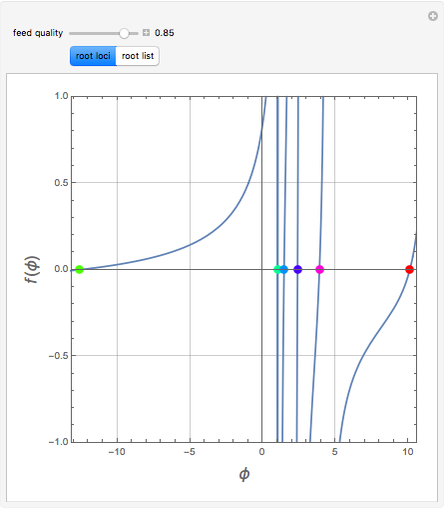
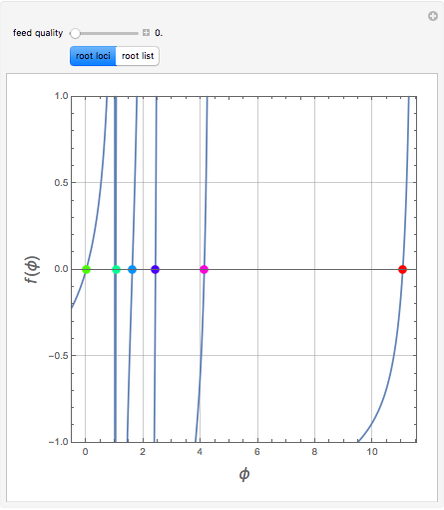
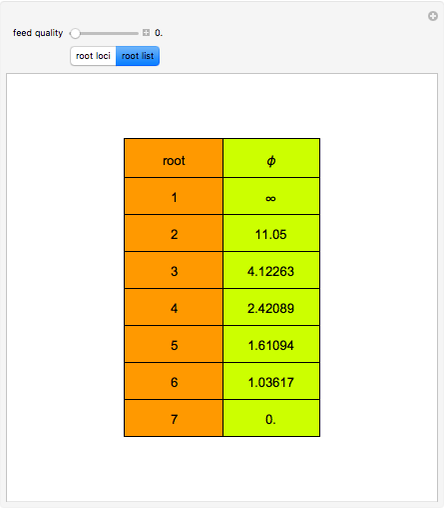
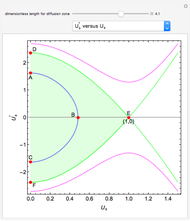
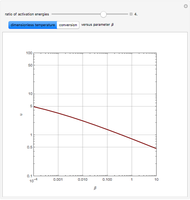
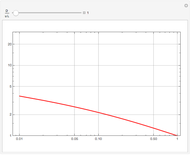
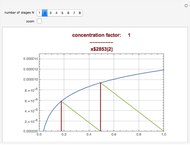
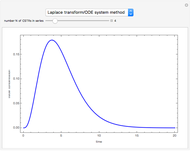
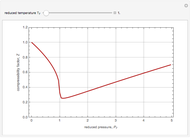
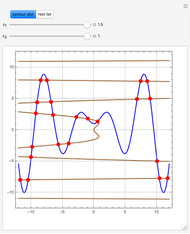
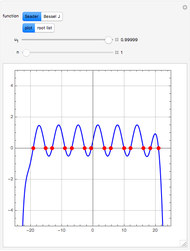
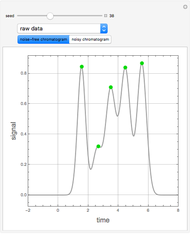
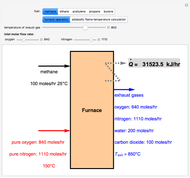
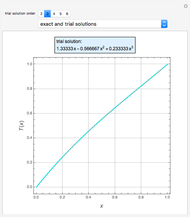
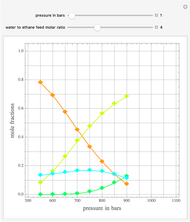
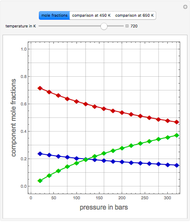
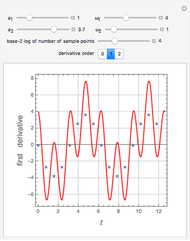
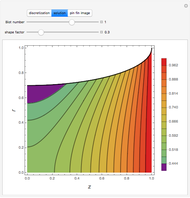
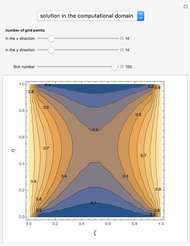
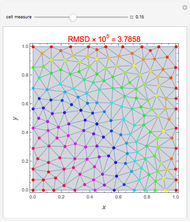
The solution to the familiar eigenvalue problem 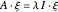 is routinely taught in undergraduate linear algebra courses, but it is rare that the generalized eigenproblem
is routinely taught in undergraduate linear algebra courses, but it is rare that the generalized eigenproblem 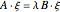 is discussed, often because of a lack of suitable physical examples where such problems arise. In this Demonstration we show how a familiar distillation problem in undergraduate chemical engineering can be reformulated as a generalized eigenvalue problem to find the roots of an
is discussed, often because of a lack of suitable physical examples where such problems arise. In this Demonstration we show how a familiar distillation problem in undergraduate chemical engineering can be reformulated as a generalized eigenvalue problem to find the roots of an 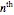 -order polynomial.
-order polynomial.
Contributed by: Housam Binous and Brian G. Higgins (December 2012)
Open content licensed under CC BY-NC-SA
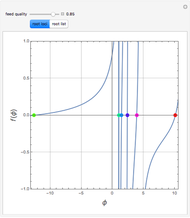
Snapshots
Details
References
[1] R. Monroy-Loperena and M. Vacahern, "Roots of the Underwood's Equations in Short-Cut Distillation from a Companion Matrix Eigenvalues," Chemical Engineering Science, 76(1), 2012 pp. 9–13. doi:10.1016/j.ces.2012.03.025.
[2] R. Monroy-Loperena and F. D. Vargas-Villamil, "Determination of the Polynomial Defining Underwood's Equations in Short-Cut Distillation Design," Industrial and Engineering Chemical Research, 40(24), 2001 pp. 5810–5814. doi:10.1021/ie010091o.
Permanent Citation