Time Encoding of Analog Signals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
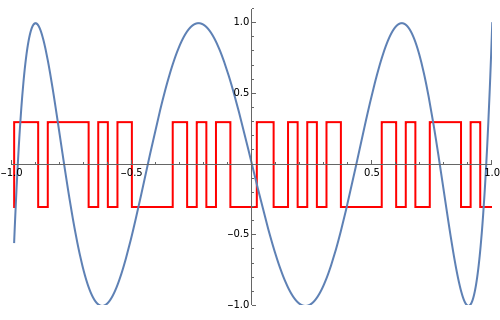
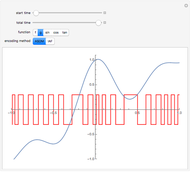
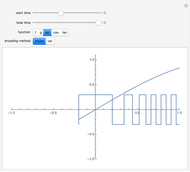
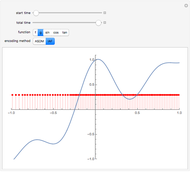
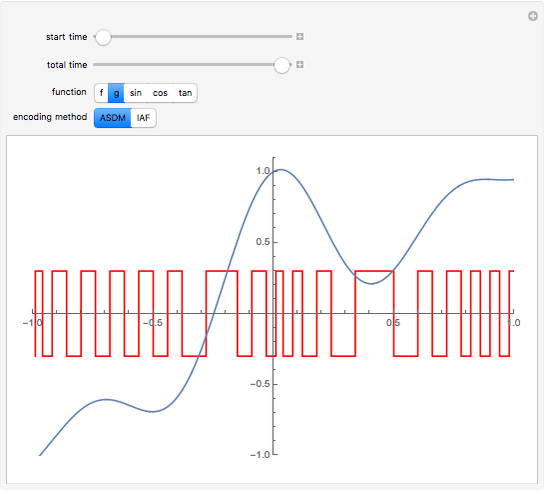
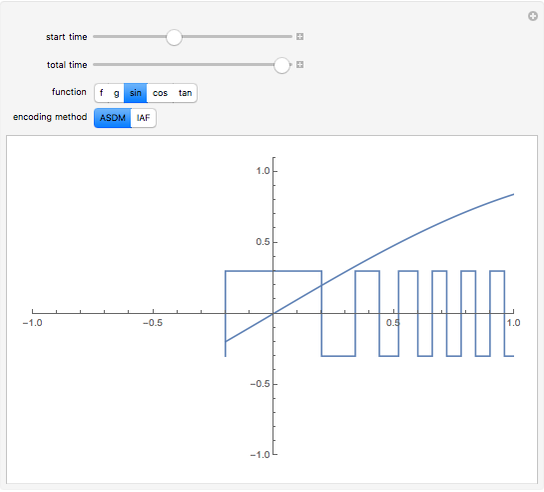
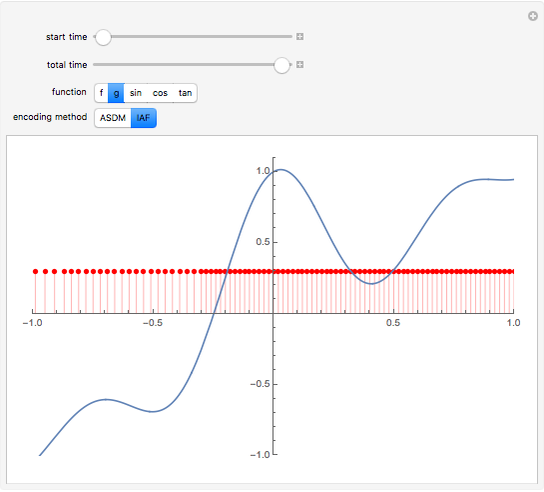
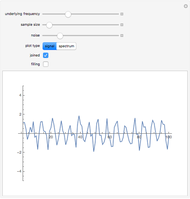
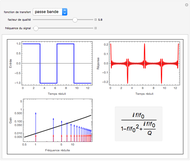
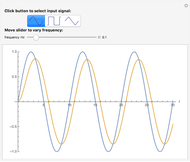
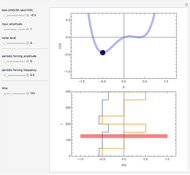
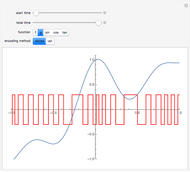
This Demonstration illustrates the process of time-encoding an analog signal. With the integrate-and-fire (IAF) encoding method, the given analog signal is accepted by a neuron until it reaches a set threshold. At this point, the neuron fires, producing a spike. Thus, when the analog signal input is stronger, spikes are emitted more frequently. This sequence of spikes is the time-encoded form of the original analog signal, and in fact it encodes all information about the analog signal as long as it is a band-limited signal. With the asynchronous sigma-delta modulator (ASDM) encoding method, the output is instead a modulated signal dependent on the amplitude of the initial analog signal. Manipulating the starting time of the encoding shows that the same analog signal has completely different time encodings depending upon the range of time over which the signal is encoded.
Contributed by: Andre Kessler (January 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration was based on [1] and inspired by the Bionet Laboratory's Time Encoding and Decoding Toolbox [2]. The first two sample analog functions, 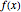 and
and 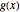 , are the seventh-degree Chebyshev polynomial and
, are the seventh-degree Chebyshev polynomial and 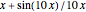 , respectively.
, respectively.
Snapshot 1: encoding of sample function 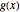 via an ASDM
via an ASDM
Snapshot 2: encoding of 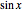 over a limited domain via an ASDM
over a limited domain via an ASDM
Snapshot 3: encoding of sample function 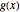 via an IAF
via an IAF
References
[1] A. A. Lazar, "A Simple Model of Spike Processing," Neurocomputing, 69, June 2006 pp. 1081–1085. http://www.sciencedirect.com/science/journal/09252312.
[2] L. Givon, Time Encoding and Decoding Toolbox Documentation. (June 2010) bionet.ee.columbia.edu/code/ted.
Permanent Citation