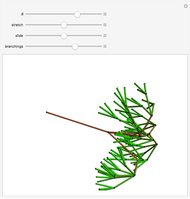
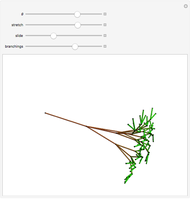
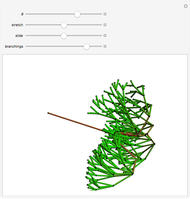
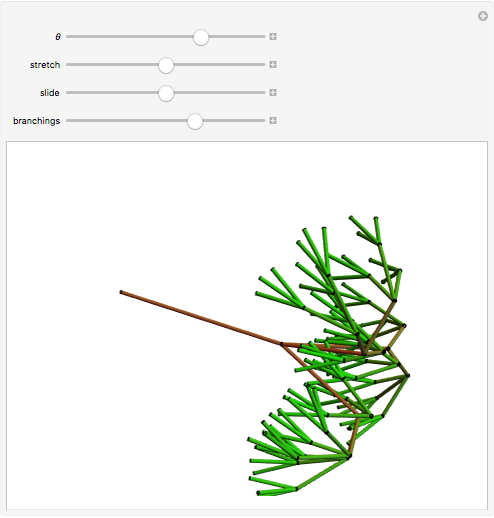
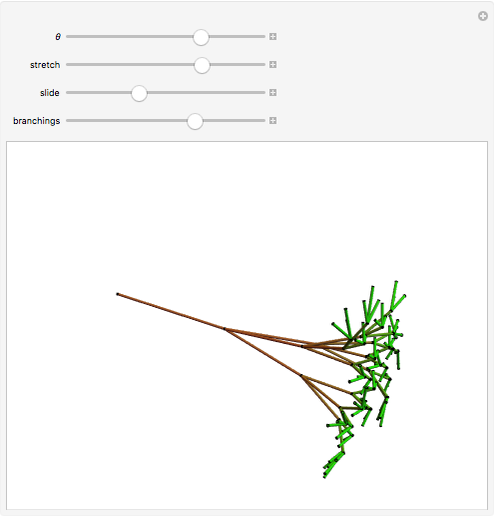
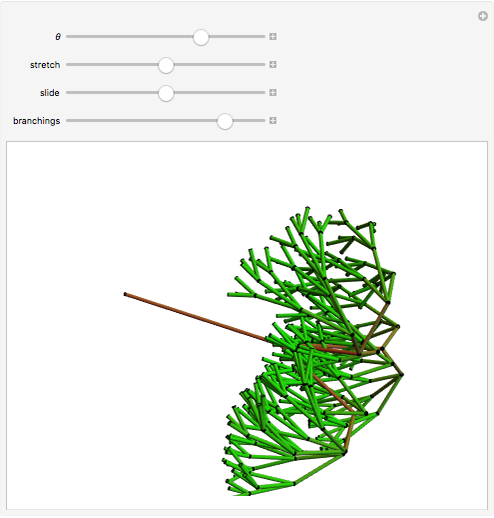
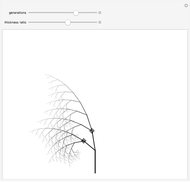
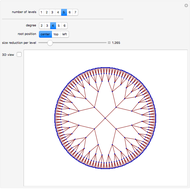
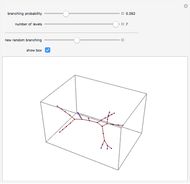
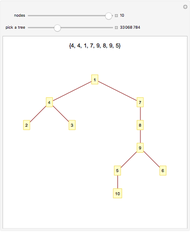
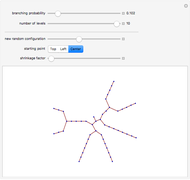
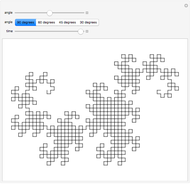
In 4D, multiplication by quaternions gives a linear transformation, which ensures that the branches have the same lengths relative to their trunk, and the same angles, regardless of the orientation of their trunk. The same thing happens in 2D with complex multiplication, but in 3D such a transformation is not possible, which is not unrelated to the forced vanishing of vector fields on the sphere. In this Demonstration, the fourth dimension, serving as a hidden variable, is used to color the edges for even more visual interest. The hidden fourth dimension plays a key role in maintaining the symmetry of the branchings, unlike its 3D counterpart. One can think of the Demonstration as occurring in 4D and imagine that the variable theta determines the angle the branches take from their parent branch.
Browse all topics
