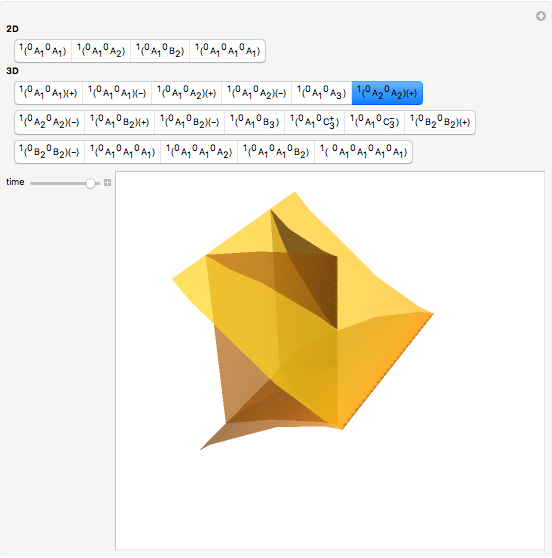
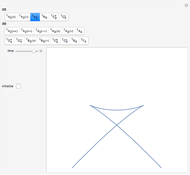
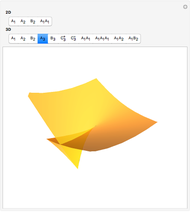
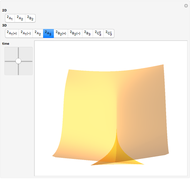
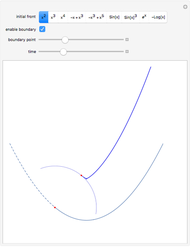
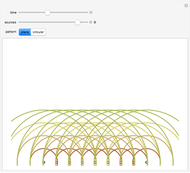
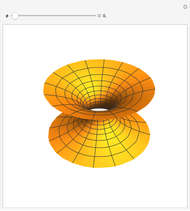
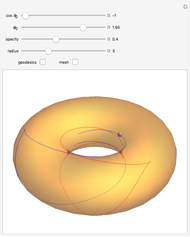
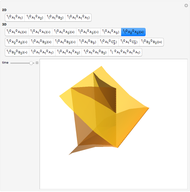
Typical Bifurcations of Wavefront Intersections

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration shows all generic bifurcations of  intersections of wavefronts generated by a hypersurface with or without a boundary in a smooth
intersections of wavefronts generated by a hypersurface with or without a boundary in a smooth  -dimensional manifold for
-dimensional manifold for  ,
,  . The time can be varied with a slider.
. The time can be varied with a slider.
Contributed by: Takaharu Tsukada (April 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In this Demonstration, stable reticular Legendrian unfoldings and generic bifurcations of wavefronts are generated by a hypersurface germ with a boundary, a corner, or an r‐corner (cf. [4]).
For the case  , the hypersurface has no boundary; the fronts are described as perestroikas (in [1] the figures are given on p. 60). A one-parameter family of wavefronts
, the hypersurface has no boundary; the fronts are described as perestroikas (in [1] the figures are given on p. 60). A one-parameter family of wavefronts  is given by a generating family
is given by a generating family  defined on
defined on  such that
such that 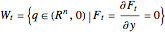 .
.
For the case 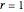 , the hypersurface has a boundary; a reticular Legendrian unfolding gives the wavefront
, the hypersurface has a boundary; a reticular Legendrian unfolding gives the wavefront  , where the set
, where the set  is the wavefront generated by the hypersurface at time
is the wavefront generated by the hypersurface at time  and the set
and the set  is the wavefront generated by the boundary of the hypersurface at time
is the wavefront generated by the boundary of the hypersurface at time  .
.
A reticular Legendrian unfolding has a generating family. Then the wavefront  is given by the generating family
is given by the generating family  defined on
defined on  such that
such that 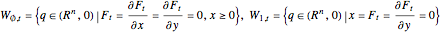 .
.
Typical bifurcations of wavefronts in 2D and 3D are defined by generic reticular Legendrian unfoldings for the cases  . Their generating families are stably reticular
. Their generating families are stably reticular  ‐
‐ ‐
‐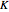 ‐equivalent to one of the following.
‐equivalent to one of the following.
For  :
:
 ,
,
 ,
,

For  :
:

Typical wavefronts in 2D and 3D are shown for  singularities while typical bifurcations in 2D and 3D are shown for
singularities while typical bifurcations in 2D and 3D are shown for  singularities.
singularities.
The author also applies the theory of multi-reticular Legendrian unfoldings in order to construct a generic classification of semi-local situations.
A multi-reticular Legendrian unfolding consists of  products of reticular Legendrian unfoldings. Its wavefronts are unions of wavefronts of the reticular Legendrian unfoldings.
products of reticular Legendrian unfoldings. Its wavefronts are unions of wavefronts of the reticular Legendrian unfoldings.
A multi-generating family of a generic multi-reticular Legendrian unfolding ( ) is reticular
) is reticular  ‐
‐ ‐
‐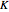 ‐equivalent to one of the following:
‐equivalent to one of the following:
 .
.
References
[1] V. I. Arnold, Singularities of Caustics and Wave Fronts, Dordrecht: Kluwer Academic Publishers, 1990.
[2] V. I. Arnold, S. M. Gusein–Zade, and A. N. Varchenko, Singularities of Differential Maps I, Basel: Birkhäuser, 1985.
[3] T. Tsukada, "Genericity of Caustics and Wavefronts on an r-Corner," Asian Journal of Mathematics, 14(3), 2010 pp. 335–358.
[4] T. Tsukada, "Bifurcations of Wavefronts on r-Corners: Semi-Local Classifications," Methods and Applications of Analysis, 18(3), 2011, pp. 303–334.
Permanent Citation