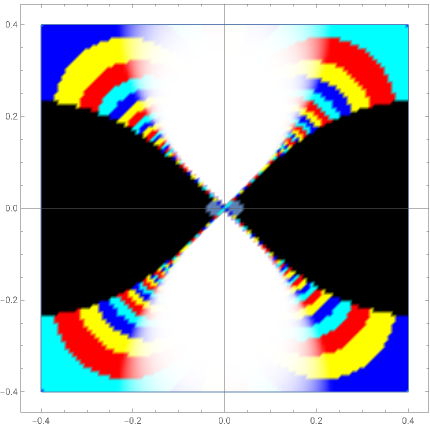
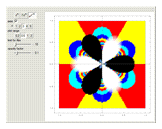
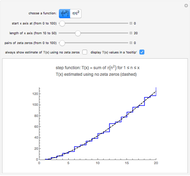
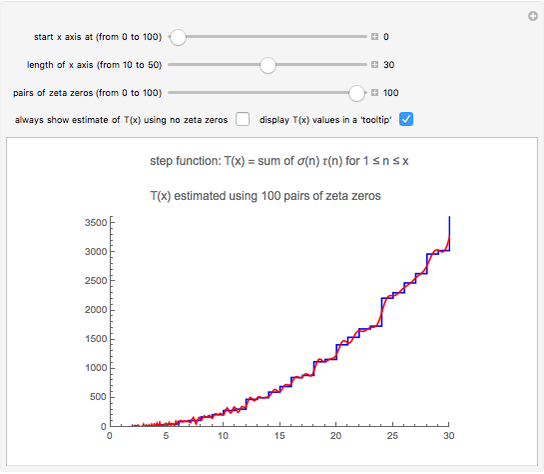
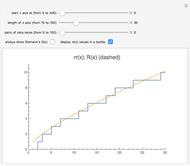
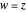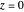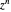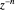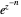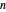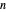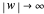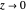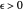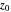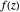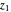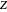Zeros, Poles, and Essential Singularities
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
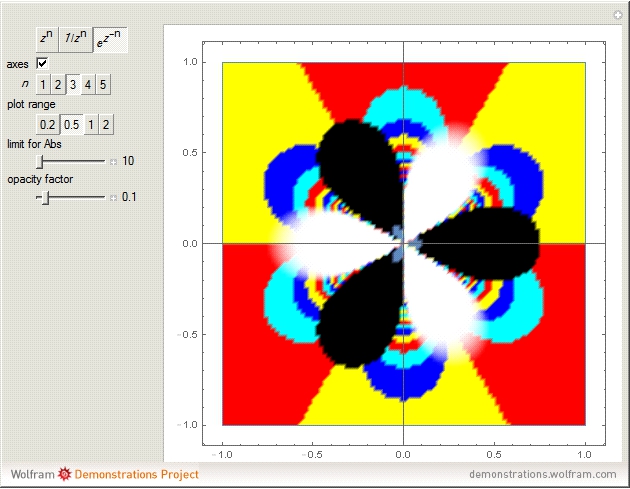
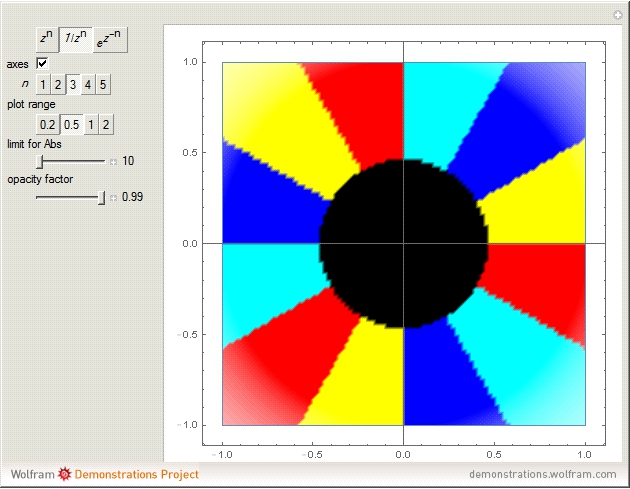
Let 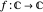 be a complex-valued function. Assign a color to each point
be a complex-valued function. Assign a color to each point  of the complex plane as a function of
of the complex plane as a function of 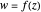 , namely the RGB color with four arguments
, namely the RGB color with four arguments  ,
, 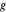 ,
,  , and
, and 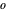 (red, green, blue, and opacity, all depending on
(red, green, blue, and opacity, all depending on 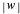 ). If
). If 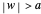 (with
(with 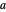 chosen by its slider), use black. Otherwise: if
chosen by its slider), use black. Otherwise: if 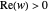 ,
, 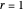 ; if
; if 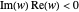 ,
, 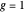 ; if
; if 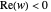 ,
, 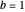 .
.
Contributed by: Izidor Hafner (February 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] A. Sveshnikov and A. Tikhonov, The Theory of Functions of a Complex Variable (G. Yankovsky, trans.), Moscow: Mir Publishers, 1971.
Permanent Citation